Calculus has a very rich history. It had a troubled birth when it was "invented" by Newton and Leibniz at almost the exact same time. This was a complete coincidence as Leibniz was working by himself in Germany and Newton was by himself in England. The two had heated conversations with each other, each trying to prove that they invented calculus.

It all came down to the president of the Royal Society to decide who invented Calculus. The president gave Newton the credit of inventing it. I say the decision was a bit unfair since Newton, himself, was the President...

Anyway, Leibniz was disheartened. He did get the credit for the first published work on Calculus, so he had that going for him.

The thing is, the calculus we use today is the Newtonian once. Newton's method was a lot easier to understand and use compared to Leibniz's. So, from it's very creation, calculus has changed very little, if at all.

The applications of calculus are a bit preserved and specific. It isn't something you yourself use everyday, but a lot of things around you has had calculations done to it, most of it being calculus.

Electrical circuits consisting of resistors, inductors and capacitors require calculations through calculus to determine the current flow and voltage difference at various points and between various components. Another real life application is in cars.

The suspension system of a car utilises a "mass spring damper" system. The mass being that of the car itself. The springs, you can see if you look just behind the tyres and the damper is that shaft right in the middle of the spring. The three work together to dissipate any unwanted energy delivered to the car from the bumpy roads. Well, the mass of the car is what "creates" the energy. The spring then acts against it to absorb the energy and the damper dissipates it. You make be asking how this is even related to calculus? Well, we can look at the forces acting on that system using this model.

Using Newton's second law, we know that:

F(m) = ma

Here, F(m) = Force, m = mass, a = acceleration

Second thing, one we may not know, is that force exerted by a damper is proportional to the velocity at with the damping mechanism (often a piston) is moving inside a damper. This is given by:

F(b) = bv

Here, F(b) = Force, b = damping factor, v = velocity of piston

And third, the spring. Hooke's law states that the longer the elongation or compression of a spring, the more force the spring exerts. Using this, the following can be derived:

F(k) = kx

Here, F(k) = Force, k = spring constant (different for every spring), x = distance/displacement (compression or elongation)

Now, we know that for a system in equilibrium, the sum of the forces is always equal to zero. From this, we can say:

F(m) + F(b) + F(k) = 0

or

ma + bv + kx = 0

Now, here's the clever part.

We know that x is a distance. We can leave it as that. We know that velocity is the change of distance with respect to time. In other words, speed = distance/time. We call this the rate of change of distance with respect to time. dx/dt. We'll call it x' because it is easier to write.

And acceleration is velocity divided by time. Just as before, we call this the rate of change of velocity with respect to time. dv/dt. But we know that v = dx/dt. So, we can write dv/dt as (d/dt)(dx/dt) = ((d^2)x)/(dt^2). This is the first derivative of velocity, or the second derivative of distance. We can call this v' or x''. However, since everything is in terms of x, we'll call it x''.

Substituting these back into the equation, we have our second order ordinary differential equation:

mx'' + bx' + kx = 0

To many of us, it looks like a quadratic equation, and in a sense, that what it is. Given the values of m, b and k, the nature of response to a "step" can be determined. A "step" being an instantaneous force applied to the system. The most interesting observation that can be made is that the value of "b" has an effect of how quickly the damping occurs.

E.g. let's say you are in a car. It goes over a pothole (hole on the road, I don't know what it's called in other countries). You don't want it to get damped too quickly. This is because if it's damped too quickly, it would almost have the same impact as having no suspension at all. You will probably be slightly thrown around in the car, and it will not be pleasant. It will probably hurt slightly. You don't want it to dampen slowly either. Why? Well, let's say you're in the car and it does over the pot hole. The damper needs to dissipate the energy or else the spring will keeping going up and down. You'll be in that car, and it will bobbing up and down for a very long time. It will probably make you feel sick. That's why, the right amount of damping is required.

However, sometimes, we don't want damping. An example is when using things like pendulums. Pendulums are designed to swing for as long as possible, and were used to keep the time. What do you do when you don't want to lose any energy from damping? You get the rid of the damper, essentially making "b" zero. This will result in:

mx'' + kx = 0

letting x = cos (wt),

x' = -w*sin(wt)

x'' = -w^2 * cos(wt)

Substituting back into the equation, we get:

-mw^2 * cos(wt) +k*cos(wt) = 0

We can eliminate cos(wt) and be left with:

w = (k/m)^1/2

Here, w is the angular velocity of the object in motion. Using w = 2*pi*f, we can find f (frequency) of oscillation of the object.

Things these is where calculus is used physically. Another place where calculus can be used is in multidimensional motions e.g. diffusion and heat transfer.

By this, I mean particles will be moving in multiple dimensions are multiple velocities. This required more than one variable. The calculations in these fields are termed "multi-variable calculus" and utilises partial differential equations.

Some famous and commonly used examples are:

The Laplace equation: 

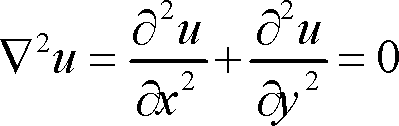
The Wave equation:

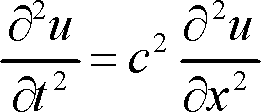
The Heat Equation: 

All three PDEs have their own way of being solved, and aren't significantly different from solving ODE's.

Calculus is often deemed the pinnacle of applied mathematics as almost all calculations require either Calculus or Linear Algebra. Modelling of systems in Engineering and Physics often utilise various principles from Calculus.

Funnily enough, the one I am the most uncomfortable with to this day is first order ODE's. 

RC (Resistor Capacitor) circuits use first order ODE's to solve for currents and voltages. Often, higher order ODEs can be converted to 1st order by converting them into their "space state" form. This is one of those times where Calculus and Linear algebra work hand in hand.

To summarise, calculus can be found in nature, it can be found in man-made things. Calculus governs the way everything works relative to something else. May it be distance with time or temperature with velocity. Anything that can experience a change if something else is changed can have calculus applied to it.

Of course, I haven't fully explored the field of Calculus, but it is still one of the most interesting subjects for me.

Here, I was given a first order ODE to solve by EnigmaUnseen and to be honest, it did take quite a while, but I eventually got there. There are two ways of solving a first order ODE: separation of variables and integrating factor method. This one didn't require an integrating factor, but did require a substitution.

Well, here's the question:

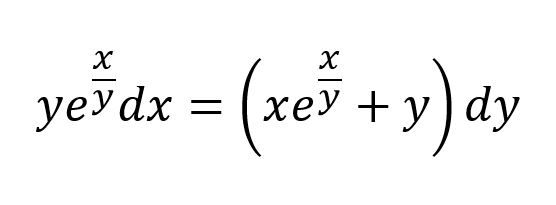
And the answer:

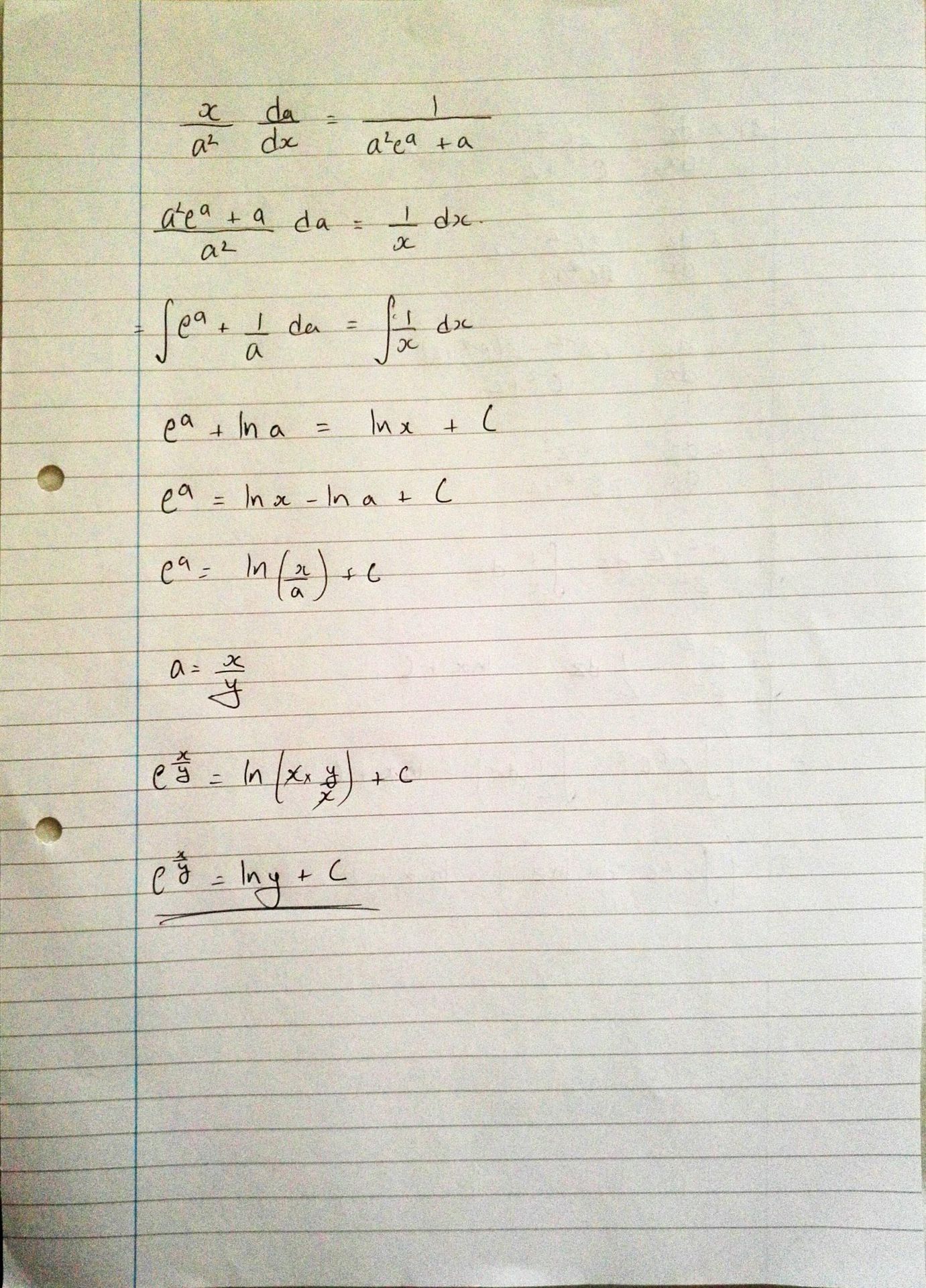
Well, thanks for reading! Please don't hesitate to send in more!