Algebra can be considered the back bone of applied Mathematics. It is used in our daily lives, e.g. buying something from the shops.

You buy 10 apples costing £1 each and 3 books costing £3 each. Using simple algebra, you can easily determine that you will be spending £19 buying all of that. The price can vary. Let's say the books were on sale, for £2. This means that now, you'll be spending £16 instead.

I can set the price of the objects as variables and number of objects as constants. In this case:

a = price of apples
b = price of books

T = total cost

This means that I can drive an expression for the total cost as:

10a + 3b

Now, I can equate that to the total cost to end up with an equation:

10a + 3b = T

This is what almost all of algebra is. It gets progressively more difficult, but the basis is the same. There are variables, and there are constants, and they're all equal to something.

To solve an algebraic equation, they should provide the same number of equations as there are variables. By that, I mean, take the example above:

10a + 3b = T

Let's use the first numbers where "a" was £1 and "b" was £3. From that, we know that T = £19.

We end up with:

10a + 3b = 19

Currently, there is no way yo find a solution for the above problem. By that, I mean if I were to give you just that expression, and nothing else, in a blank page, you will never be able to find the values of a and b as it is impossible. This is because you have two unknown variables, being a and b, while you're only given one expressions.

To avoid this, another algebraic equation can be given. For example, lets say someone else goes into the store and buys one apple and one book, this means that they will play £4. Hence, we can model it by as follows:

a + b = 4

You now have two distinct equations. In other words, One equation is not dependent on the other.

By that, I mean:

2a + 2b = 8

and

a + b = 4

These two are dependent on each other, so even though you are given two equations, it will be impossible to solve as the two equations are basically the same. These equations are termed "homogeneous". One is just a multiple of the other, and when that happens, it's basically as if you are given the same equation twice... which is utterly useless.

Now, going back to:

10a + 3b = 19

and

a + b = 4

There are two ways of solving this. One of them is elimination, and the other is substitution. There is a third way that utilises Matrices. It is not necessary for 2 equations, but when it gets to 7-8 equations with 7-8 variables, it becomes a lot quicker and a lot easier.

Substitution:

So, I have

10a + 3b = 19

and

a + b = 4

From this, I can rearrange the second equation to be:

b = 4 - a

I can then substitute this "b" into the first equation:

10a + 3b = 19

since b = 4 - a,

10a + 3(4 - a) = 19

10a + 12 - 3a = 19

7a = 7

a = 1

We know this is true because we set the price of apples to be 1.

Now, we know that b = 4 - a

Since we know that a = 1, we can substitute this back into the equation above:

b = 4 - 1

b = 3

And we know that the price of books is 3.

Elimination:

Again:

10a + 3b = 19

a + b = 4

Now,

if a + b = 4,

then 3a + 3b = 12

In other words, if you buy three times as many stuff, you'll have to pay three times as much.

The main objective of this multiplication is to get one of the variables from one equation to have the same coefficient as the same variable from the second equation.

In this case:

10a + 3b = 19

3a + 3b = 12

In both equations, the "b"s have the same coefficient of 3.

Now, when you subtract the two equations:

10a + 3b = 19

3a + 3b = 12
-________________

7a + 0 = 7

7a = 7

so a = 1.

So, we know that that's true.

Substitute this back into:

a + b = 4

or

10a + 3b = 19

I'll get b = 3.

That is one way to check if the answer you got is correct or not.

Let's say I made a mistake somewhere and I got a = 1 and b = 4

When I put that back in any of the two equations, I'll get:

1 + 4 = 4

or

10 + 12 = 19

Neither one of them is true as we know that:

1 + 4 =/= 4

and

10 + 12 =/= 19

If you find yourself at this state, it means that you either read the question wrong, or there is a mistake in your calculations. Do go over and start again to find the correct answer.

That's enough intro to Algebra now.

The first set of answers is a reply to Serena1799's request. If you want the questions, please do have a look in her "Some Random Stuff" book. Here are the answers:

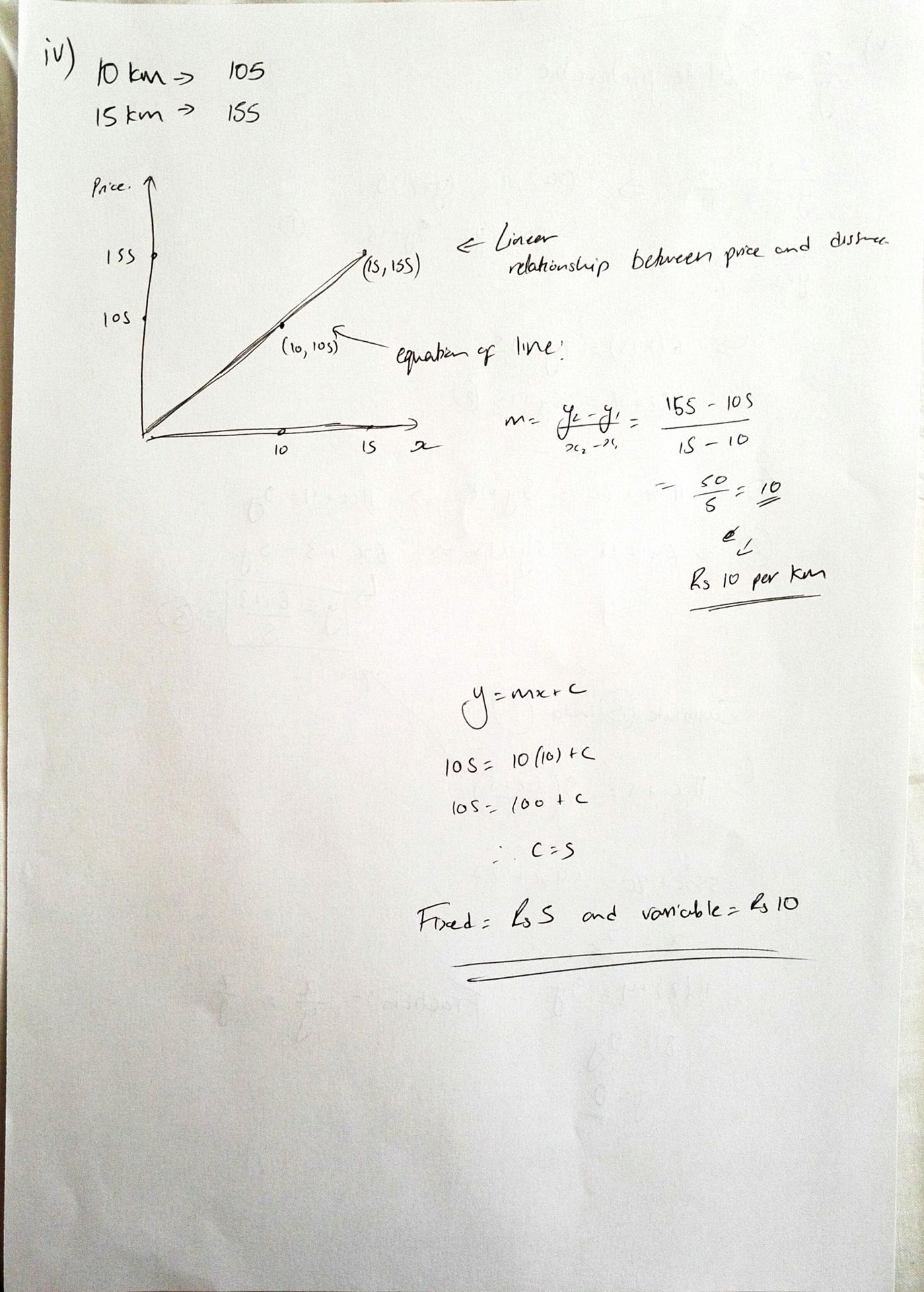
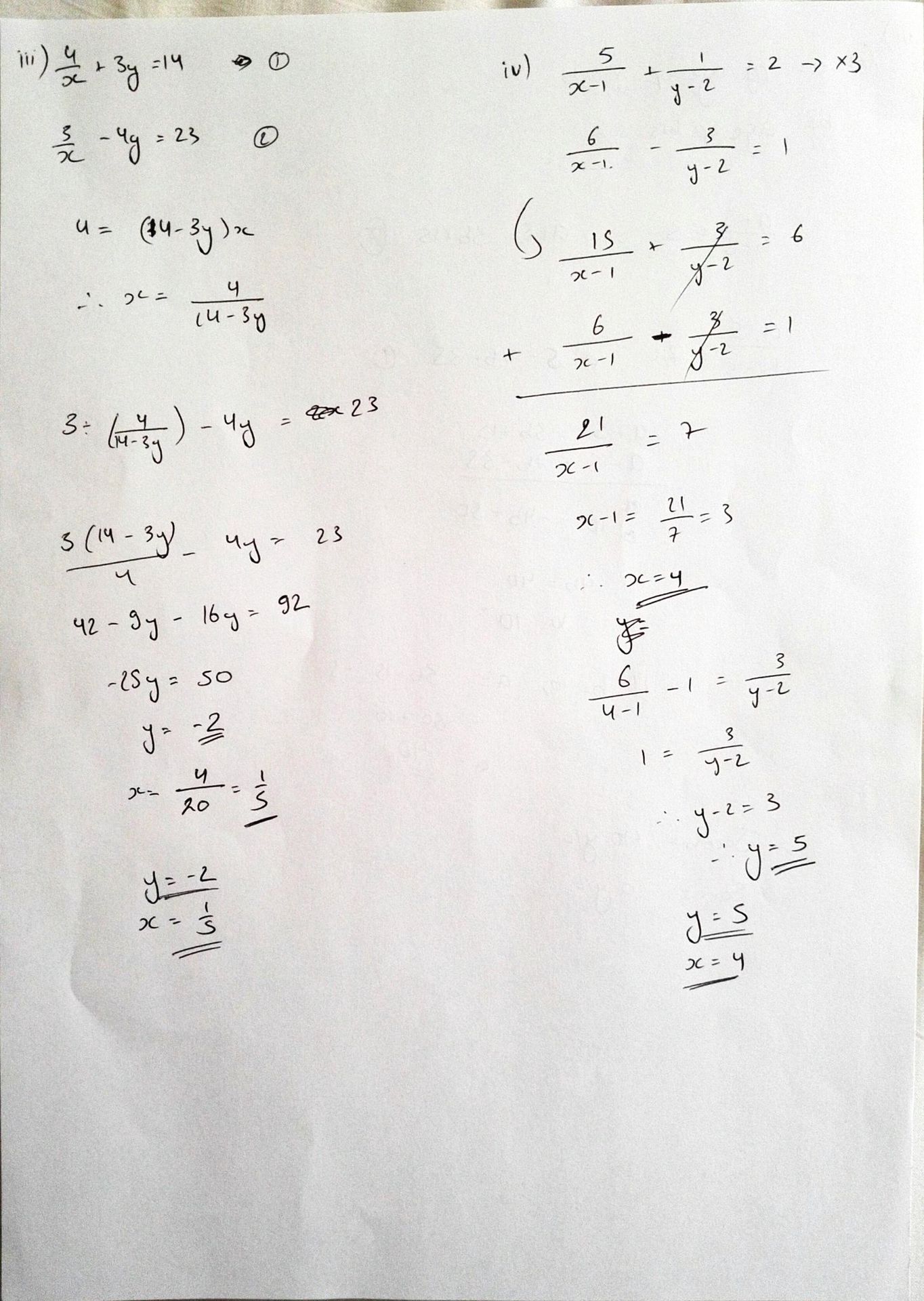
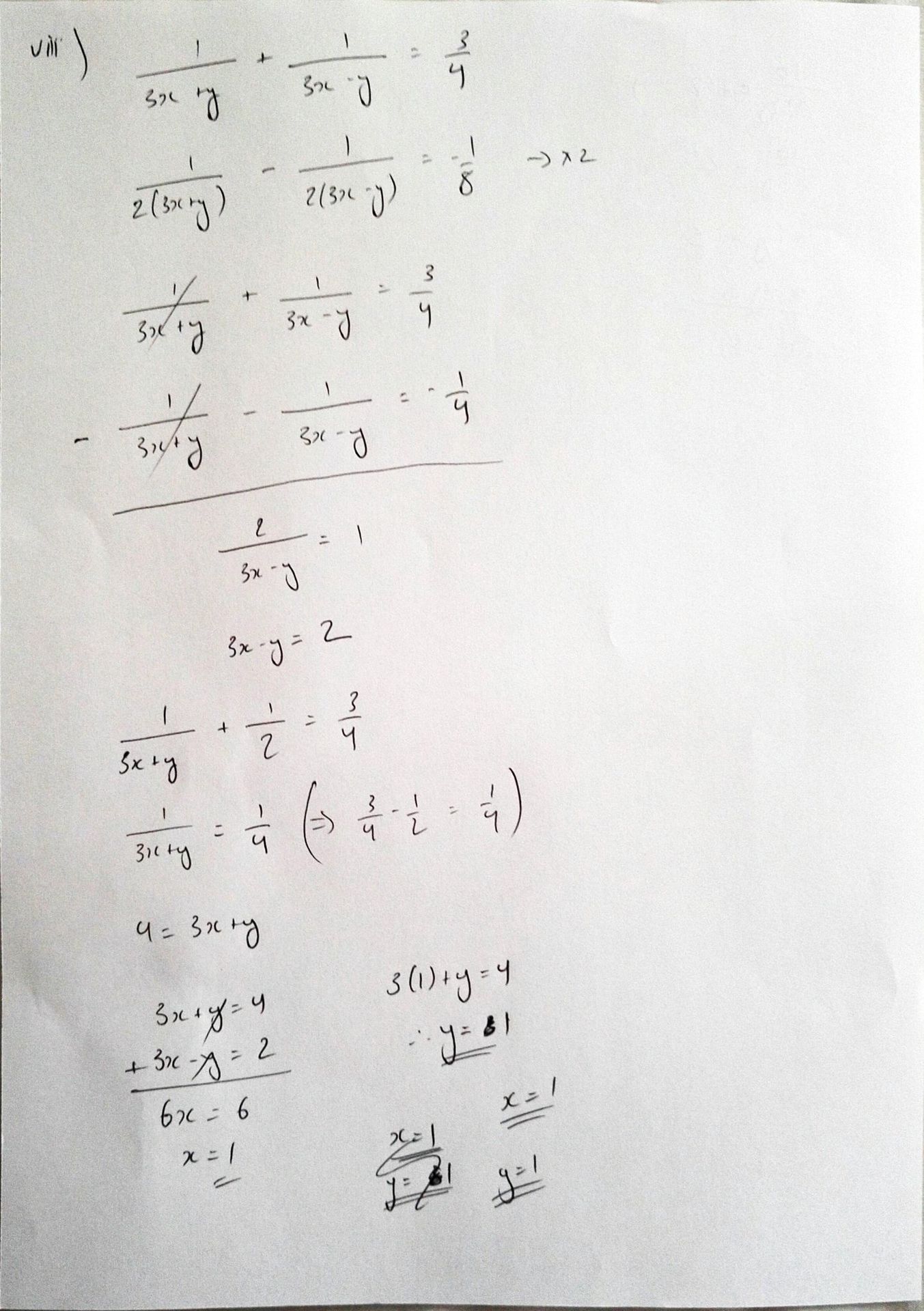
Excuse my crappy handwriting xD

Alright, that should be it. If it is difficult to read, so if something isn't clear, please do let me know. Thanks!

And send in any requests if you have some. I'm getting bored sitting here doing nothing.