What are Science laws?

I've already talked about the difference between a science law and a science theory. Now I would like to discuss some important laws of science, especially physics.

The grandfather of all physics is Isaac Newton. His laws of gravitation and motion are something that should be memorized because they are so important.

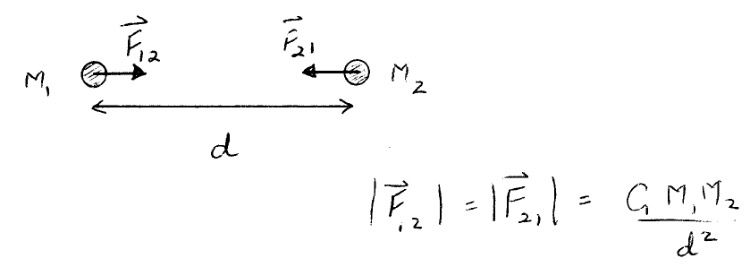
The law states F = G (m1 m2)/ r^2 or Gravity force F equals the Gravitational constant G times the m1, the mass of object 1, times m2, the mass of object 2, divided by r, the distance between the objects squared. Equations like this are basically proportionality expressions. In this case we see that the gravitational force between two massive objects in proportional to their masses multiplied together and then divided by the distance between them squared with a fudge factor thrown in to make the units work out correctly. You might wonder how Newton came up with this equation. Newton derived his equation from lots of observations and prior work by other people like Robert Hooke.

Another important law of motion describes how planets move in an ellipse with a star at one of the foci. Kepler's 1st law is r = p / 1 + e cos θ where e = √ 1 - (b/a)^2.

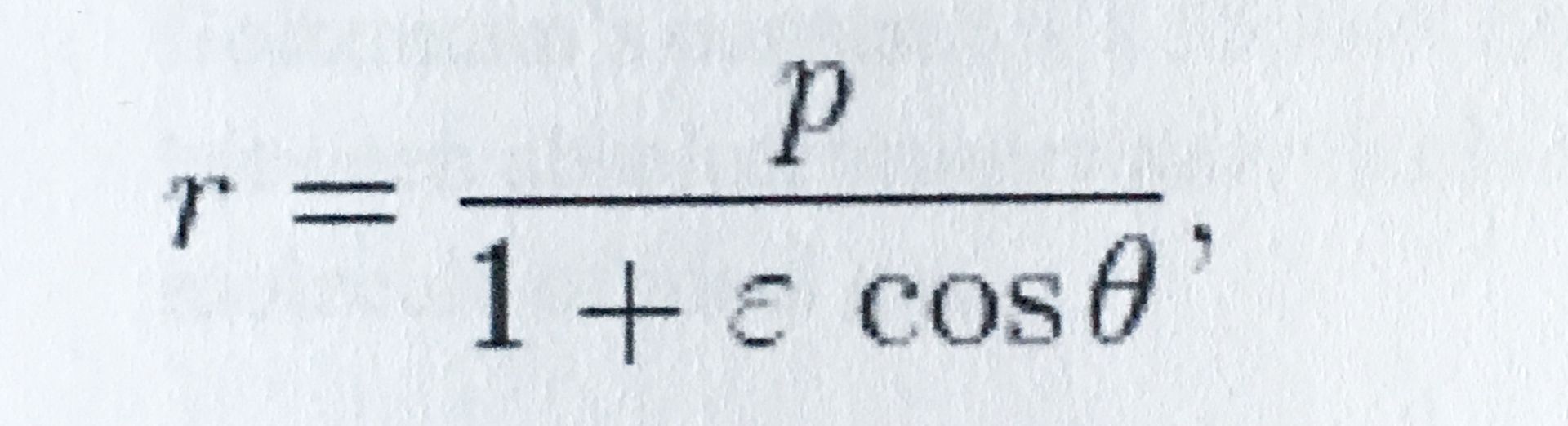
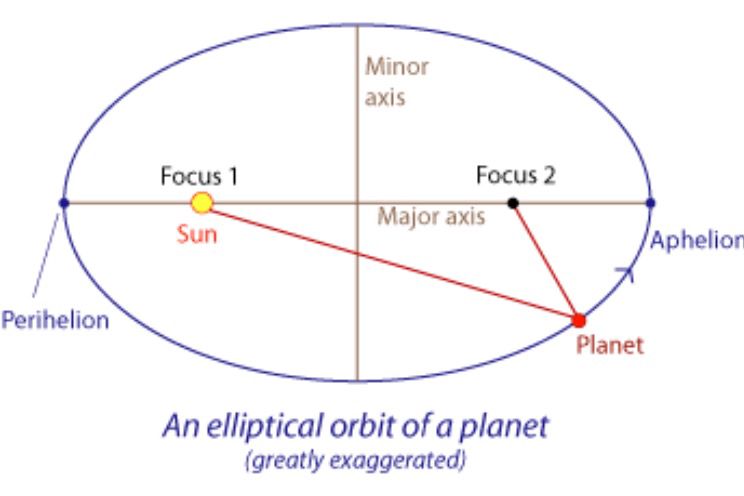
The term p is the semi-latus rectum. The latus rectum is a chord that passes through one of the foci and is parallel to major axis of the ellipse. A semi-latus rectum is half of that. The e in this equation is the eccentricity of the ellipse. The eccentricity is equal to the square root of 1 - (b/a) squared. This b divided by a part of the eccentricity equation is the ratio of the two axes. It's like the long radius divided by the short radius. The θ is the angle of the planet as in a polar coordinate or the angle from the major axis to the planet from the main loci, which is the Sun. The r that is calculated by this equation is the distance from the Sun to the planet. This equation also uses the trigonometry cosine. This important equation basically says that a planet orbiting the Sun in an elliptical path changes its distance according to trigonometry. Newton used Kepler's equations to refine his own.

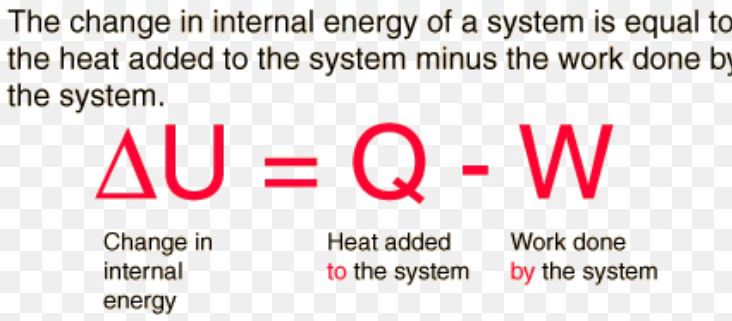
Now for something a bit easier. The first law of thermodynamics states that ΔU = Q - W which means that the increase in internal energy of a closed system ΔU is equal to the heat supplied to the system Q minus the work done on it W. What this means is that you're not going to transfer less heat to a system and expect to get more work out of it. Basically the work you get is what heat is in the system minus the heat you put into it minus the heat you get out of it. Work is seen as a process of transferring energy to or from a system to make mechanical work as in the case of a steam engine.

Now for something really theoretical but still considered a law. The time-dependent Schrödinger equation is: ihϑ/ϑtψ(r,t) = Hψ(r,t).

Time-dependent Schrödinger equation (general)

where i is the imaginary unit, h is the Planck constant divided by 2π, ϑ/ϑt represents a partial derivative with respect to time t, ψ is the wave function of the quantum system, H is the Hamiltonian operator. Basically, this equation describes how the quantum state of a quantum system changes with time. A wavefuntion is one way to describe a quantum system like an atom. A Hamiltonian operator corresponds to the total energy of a system and it's usually the sum of the kinetic and potential energies of that system. Think of it this way; let's say you're tying to consider a particle as a harmonic oscillator. Using this equation you would obtain three wave functions that satisfy the time-dependent Schrödinger equation. One wave of each function would be real, and one would be imaginary. You could also obtain the probability function for finding the particle at any given time for all three wavefunctions. These concepts led to a better understanding of quantum physics, but it was only the very beginning.

So, you see that there are some laws associated with physics, and they involve math. That's the way science works.

Thanks for reading.