Theory of Special Relativity

Einstein's special relativity theory considers the speed of light to be a constant, which is designated by c. The other aspect of this theory is that there is no inertial reference frame, but reference frames are important to the theory.
An observational frame is an observational perspective in space that is not undergoing any change in motion. A position can be designated by measuring the position on 3 axes, better know as x, y, z. Now, add a new axis that involves time and now we have a position defined by t, x, y, z. Now if an event occurs in this frame of reference, such as acceleration, one has a new position as t', x', y', z'.
t' = ϒ(t - vx/ c^2)
x' = ϒ(x - vt)
y' = y
z' = z
where  ϒ = 1/ √ (1 - v^2/c^2)  Lambda equals  one over the square root of the following: 1 minus the velocity squared divided by the speed of light squared.

This is the Lorentz factor and the process is a Lorentz transformation. One can use this equation to determine the effect of traveling near the speed of light. It becomes the fraction of the speed of light that one is traveling if moving at the velocity of v.
You can also calculate the time dilation effect by:
Δt' = ϒ Δt
This says the time between two ticks of a clock in the frame of reference that is moving near the speed of light is changed by the Lorentz factor if the clock were stationary.

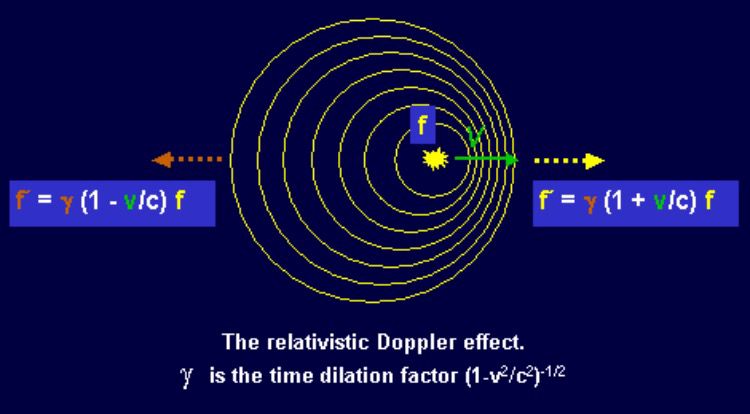
Another consequence of traveling near the speed of light is length change. In other words a stationary observer will see an object traveling that fast as being smaller in length. The amount can be calculated by using the Lorentz factor:
Δx' = Δx/ ϒ
This says that the length Δx' of a object measured in the frame in which it is moving is shorter than its stationary length Δx.
Hey, it's a new way to look thinner!

Thanks for reading.