Do the math

Mathematics is a fascinating subject that many people shy away from because it's so hard to comprehend. However, it is one of the most valuable assets to science, and it cannot be ignored, especially in astronomy.

How do astronomers use math to find things out? That's a good question. As it turns out a lot of astronomy involves math.

First example: It's fairly easy to measure the size of the Sun because it's close and appears as a disc, but how does one determine the size of stars that are further away (they are like point sources)? The answer in some cases is to use math, and in this case the method is to consider a star a black body radiator and use the Stefan-Boltzmann equation: L = 4π R^2 σSB T^4  where L is the luminosity, R is the radius, σSB is a constant equal to 5.67 x 10^-8 W m^-2 K^-4 and T is the temperature.

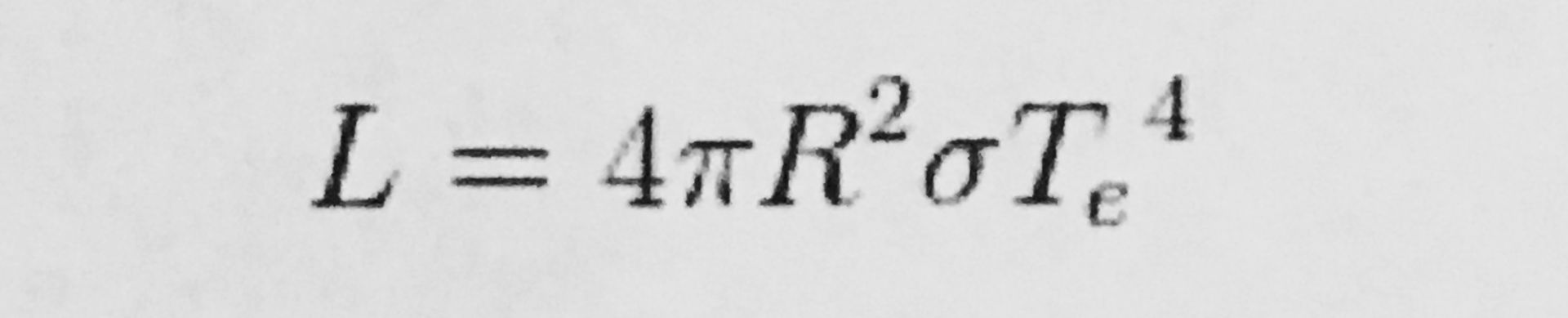
You have to know the distance to the star to use this equation because the luminosity drops with the square of the distance. The equation says that the luminosity of the star is equal to 4 times pi times the radius squared times the constant times the temperature in Kelvin to the fourth power.

Second example: Our Sun is about 4.5 Gy (billion years) old and it's half way along the main sequence, which means that it's still burning hydrogen in its core. It has another 4.5 billion years to go before the hydrogen runs out and it begins fusing helium. That means that it will no longer be stable and will go off the main sequence. Stars with higher luminosities burn quicker and don't stay on the main sequence as long. How do we calculate how long they'll stay on the main sequence? We use this formula: Tms = 10Gy (L/ L¤)^-5/7 or you could use this version.

This says that the time of a star on the main sequence is equal to ten million years times the ratio of the luminosity of the star divided by the luminosity of the Sun and this ratio to the -2.5 power.

Third example: How do astronomers determine just how bright a star is since they are at various distances away? The answer is that they us the magnitude system. The absolute magnitude of a source is its apparent magnitude at a distance of 10 parsecs. The absolute magnitude is related to the luminosity of a star.  The equation they use is: M = m - 5 log (d/10 pc).

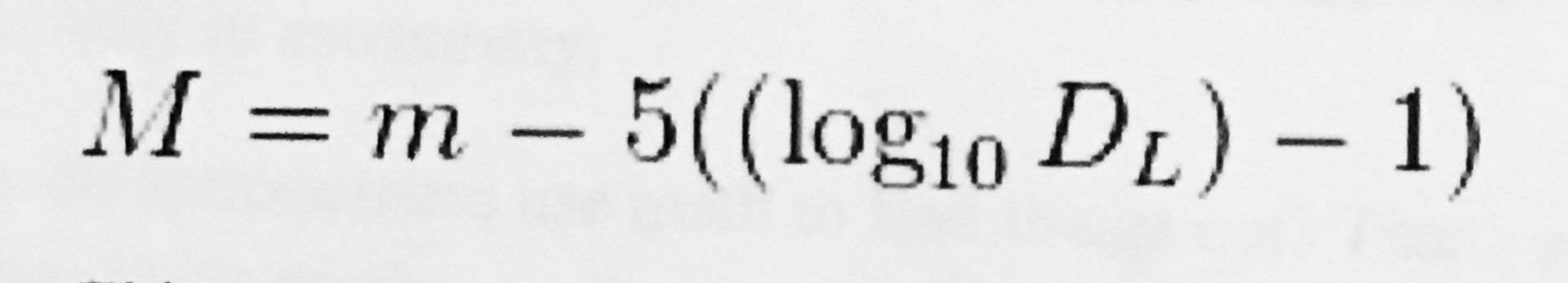
This says that the absolute magnitude M is equal to the apparent magnitude minus 5 times the log of distance (divided by 10 parsecs) or the actual distance DL in parsecs minus 1.

Fourth example: How do astronomers calculate what the gravitational forces are between two objects in space? They use the most important equation: F = G (m1 m2)/ r^2.

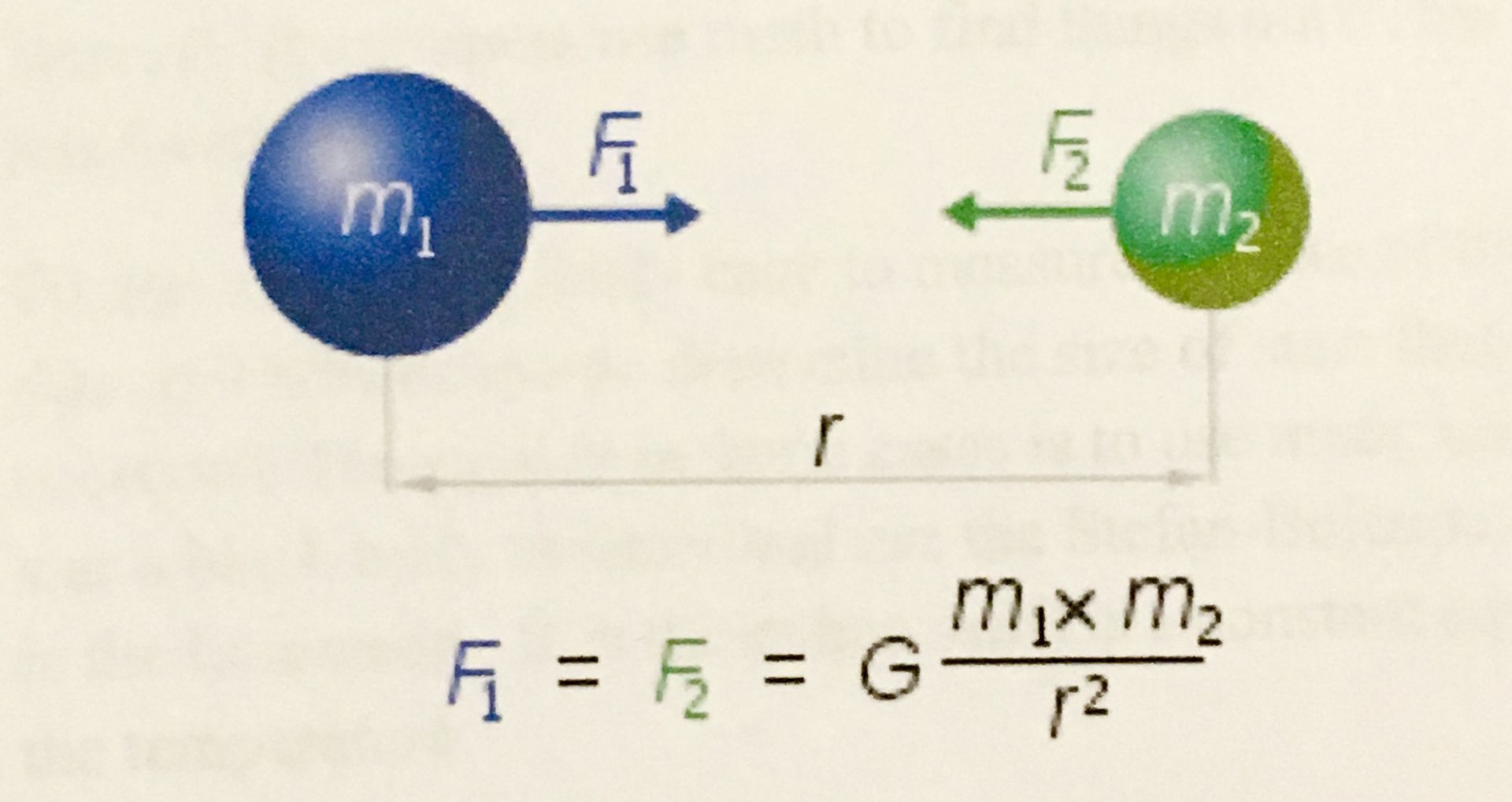
This equation says that the force between two masses m1 and m2 is equal to the gravitational constant time the ratio of mass-1 times mass-2 over the distance r between the two masses squared. That's Newton's equation and it's the one that most referred to.

I wrote this to show how math is used in astronomy. These equations are mild compared to many I've seen, but they show that much of astronomy involves calculations, calculations that often lead to great discoveries.

Thanks for reading.