Hello everyone, and welcome back! Today's lesson is on the fantastic concept of fractions.

If you ever see a number written like this: 1/2
Or this:
3
5
Or even this:
5
8
7
They're all fractions.

The thing that distinguishes a fraction is the straight line between the numerator (number on top or to the left of the line) and the denominator (number on bottom or to the right of the line).

Numerator/Denominator
Or
Numerator
Denominator

The basic meaning of this line is dividing. A fraction is just a way of writing the numerator divided by the denominator. For example, 1÷2 is written as
1
2

I believe there are two reasons why using fractions is beneficial in some cases.
1. Help you divide/write unevenly divided numbers.
2. Give a perspective to a problem that's not given by any other number form.

Reason #1

Remember from our last lesson that there are some numbers that don't divide evenly into others? For example, 2 can't go into 1 a whole number of times. This may seem troublesome, but with fractions it's incredibly easy to write the answer.

The problem is 1÷2. Remember that the straight line in fractions means division. So ÷ is the same as / .

Write the problem as a fraction: 1/2. It still means the same thing--1 divided by 2. And now that it's written as a fraction, you have an acceptable answer! The answer to 1÷2 is simply 1/2.

Important note: If you are asked to write the answer as a decimal, the fraction answer doesn't work.

Okay, so 1 and 2 are easy numbers. But fractions also help with more complicated divisions. What about 224÷56?

When you set it up as a fraction, it still doesn't look too easy.
224
40

Fractions have specific properties that can make this simpler. The most important one in this case is this:

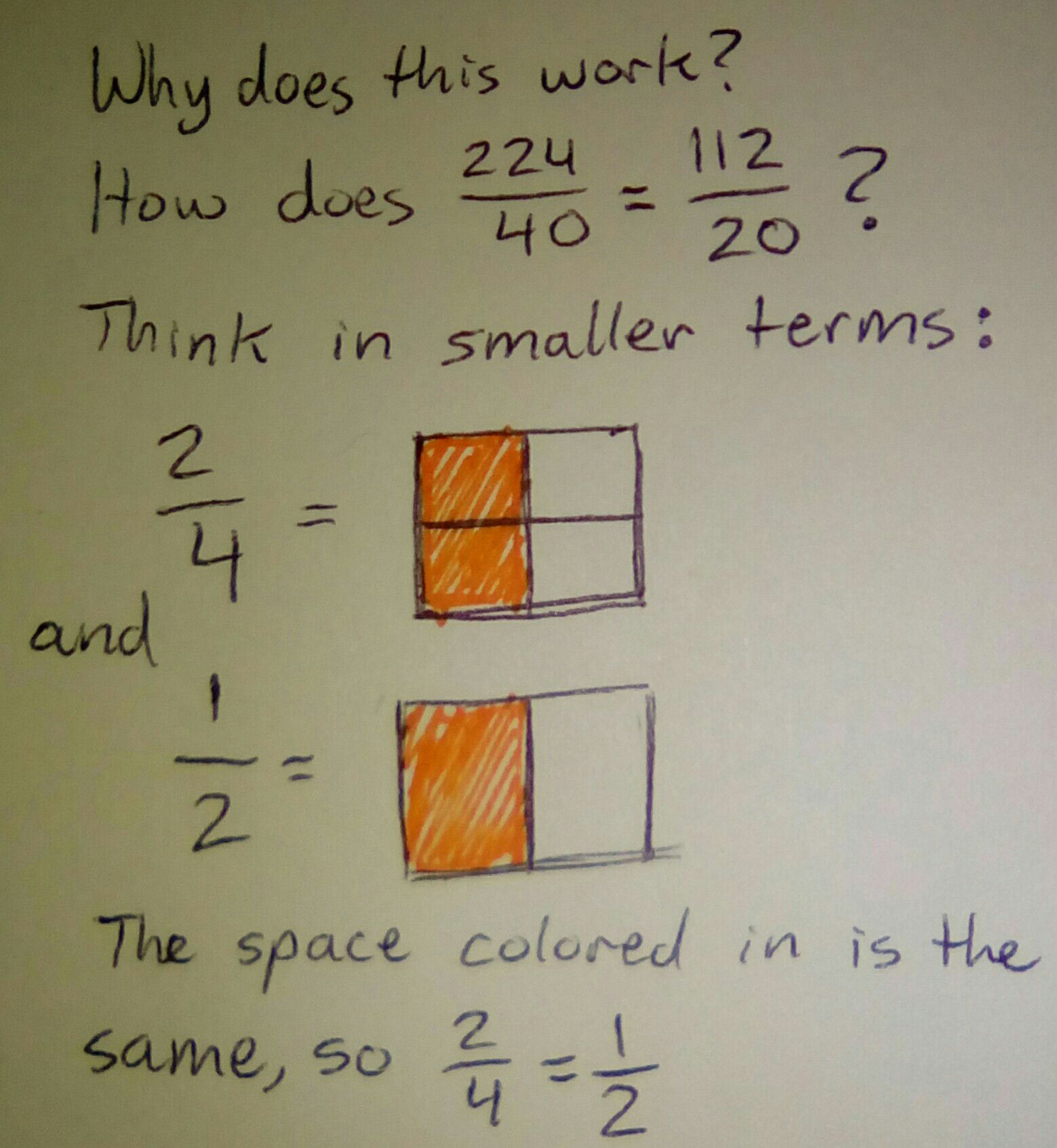
THE RULE: Any fraction may be written differently and still equal the same thing if it is altered by multiplying or dividing both the numerator and denominator by the same number.
What NOT to do:
If you change only the top, it becomes a different fraction.

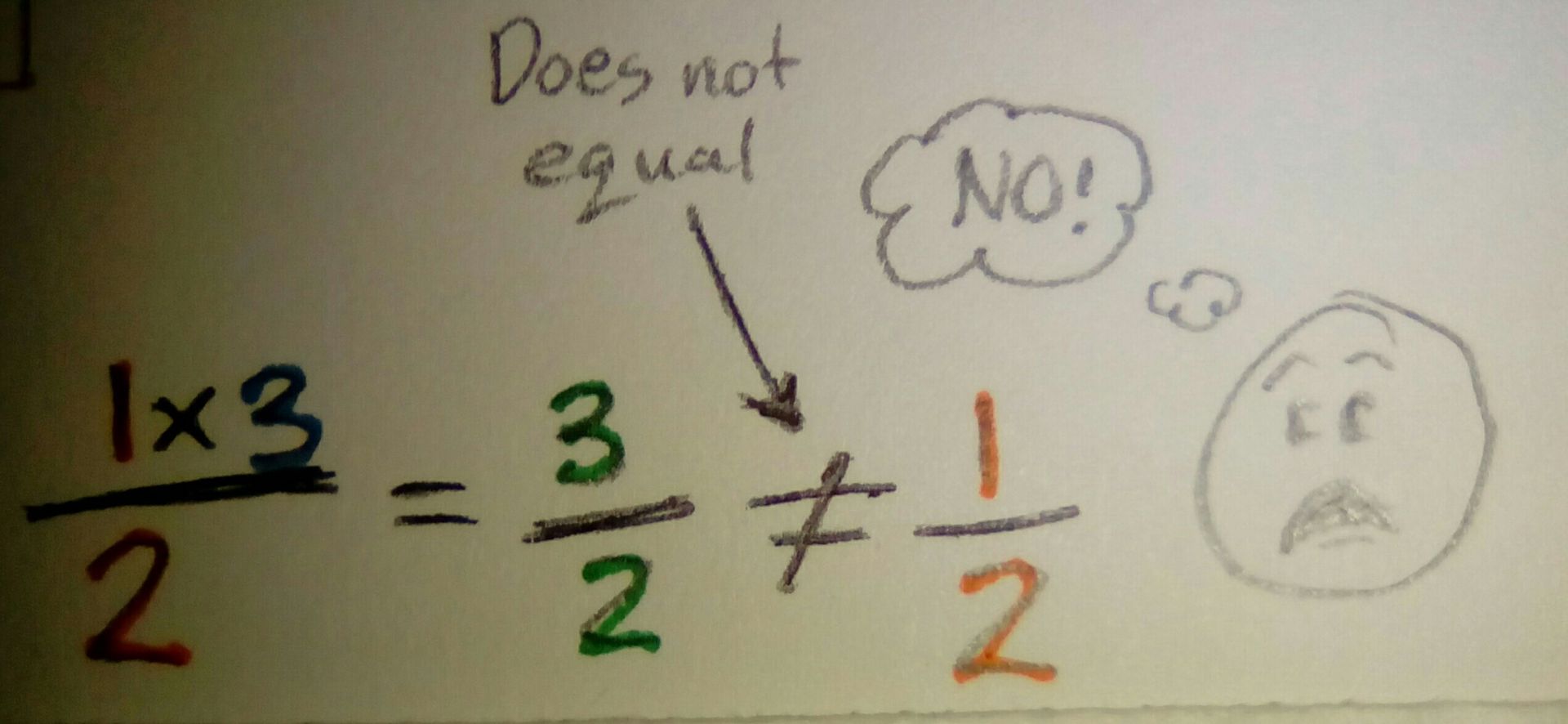
If you change only the bottom, it becomes a different fraction.

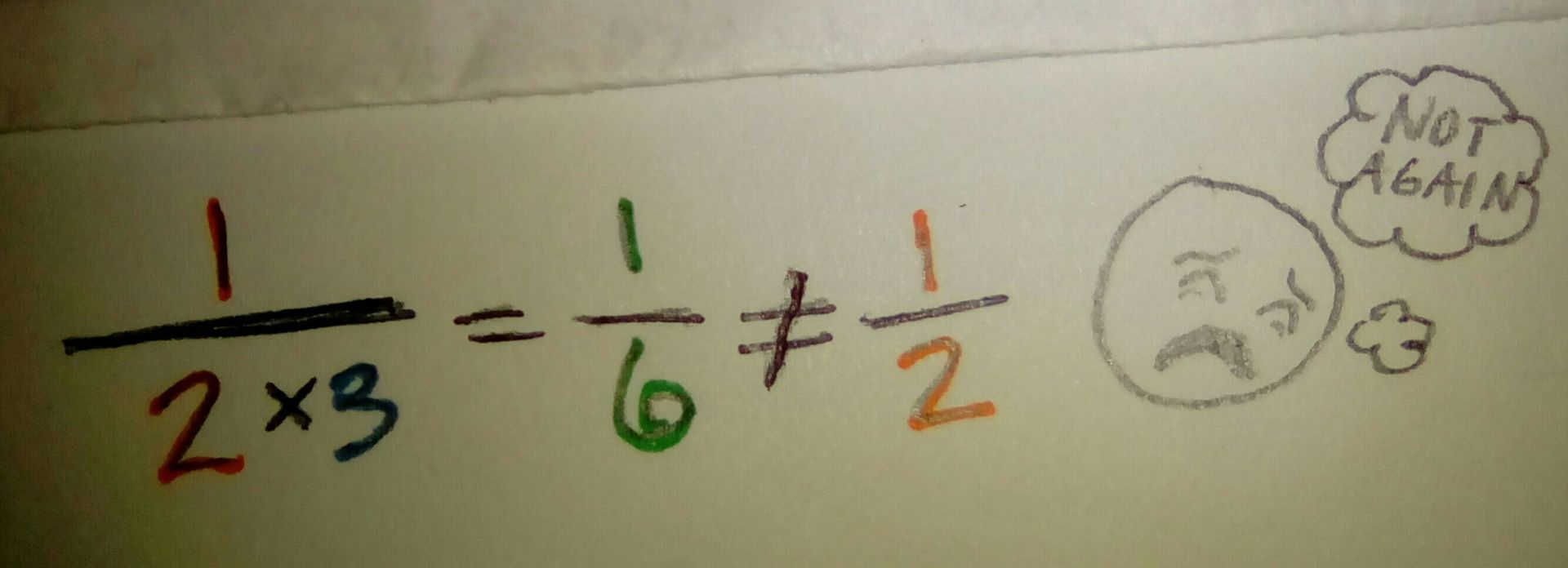
If you add to or subtract from the top or bottom, whether you add equal amounts to both, it becomes a different fraction.

Now that we know the rule, let's break this down. If you're familiar with odd and even numbers, you can immediately tell that 40 is divisible by 2, and so is 224.
224÷2=112 ➡ 112×2 Cancel ➡ 112
40÷2=20 ➡➡➡20×2 out 2 ➡➡ 20

If it's not completely simplified yet, keep going.
112÷4=28 ➡ 28×4 Cancel ➡ 28
20÷4=5➡➡➡ 5×4 out 4 ➡➡ 5

Fraction answer is 28/5

Once you get practiced enough at finding possible divisions, you can skip some steps and solve it this way:

Take a break and relax your brain. Stand up and stretch, eat a snack, and come back ready for more math. :)

In the previous lesson on division, we discussed two ways to write remainders. One of these was writing it as a fraction.

If you can recall, we took the remainder and wrote it as a fraction over the divisor.

Why do we do this? It's very simple. You divide the number as far as it can be divided evenly. Then since the remainder can't be divided evenly, you write it as fraction. How does this work? Here's another fraction rule:

So what you're doing when you divide is finding the number that the divisor can go evenly into and adding the rest as a fraction. Makes sense, right?

We're at the end of today's lesson. You may be thinking, "Wait, you said there are two reasons for using fractions, and you only did one!" You're right. I'm just saving that for another day because there's so much information I can tell you about fractions. So if you liked this lesson, you can look forward to fractions part two!

Ta ta for now!

:) Albino Kiwi