signal
Signal: Zeitlich und/oder örtlich veränderliche physikalische Größe, bei der ein oder mehrere Parameter Information tragen. Ein Signal kann mathematisch als Funktion einer oder mehrerer unabhängiger Variablen beschrieben werden. Bsp: Verkehrsampel, Spannung,...
Ein Signal ist kontinuierlich, wenn die Zeit t als stetige Variable betrachtet wird, also ein Funktionswert für beliebige Zeitpunkte im Intervall (a, b) existiert.
Ein Signal ist diskret, wenn t als diskrete Variable betrachtet wird, also Funktionswerte nur für diskrete Zeitpunkte tn definiert sind.
Ein Signal heißt stationär, wenn charakteristische Signalkenngrößen (z.B. Mittelwert, Varianz) unabhängig von der Zeit t sind.
Ein Signal x(t) ist analog, wenn es im kontinuierlichen Intervall (a, b) jeden beliebigen Signalwert annehmen kann. -> „wertkontinuierlich".
Ein Signal x(t) ist digital, wenn es nur eine endliche Anzahl unterschiedlicher Signalwerte annehmen kann. -> „wertdiskret".
Signal x(t) ist deterministisch, wenn es in analytischer Form vollständig angegeben werden kann.
Signal x(t) ist stochastisch, wenn es nicht (oder nicht vollständig) in analytischer Form beschreibbar ist.
Ein kontinuierliches Signal x(t) ist periodisch mit der Periode T, wenn für T mit T ≠ 0 gilt: x(t + T) = x(t)
Gilt dies nicht, ist das Signal transient. Die Länge von T heißt Periodendauer.
5 Merkmale des Signals: 1. zeitlich – räumlich – zeitlich/räumlich 2. kontinuierlich – diskret 3. analog – digital 4. deterministisch – stochastisch 5. periodisch – transient // 6. Symmetrie: gerade, ungerade 7. Begrenztheit, Beschränktheit, Kausalität 8. Energie und Leistungssignale
Unterschied zwischen diskret und kontinuierlich Signal
kontinuierlich: wenn die Zeit t als stetige Variable betrachtet wird, existiert ein Funktionwert für beliebig Zeitpunkt im Intervall (a, b)
diskreten: wenn die Zeit t als diskrete Variable betrachtet wird, sind ein Funktionwert tn definiert

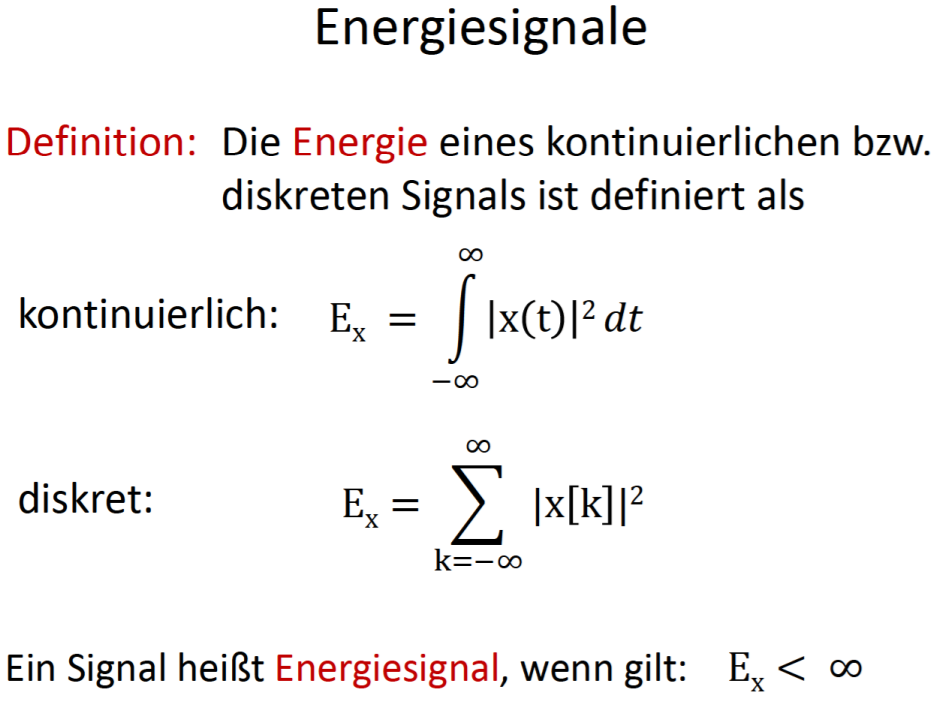
Energiesignale haben eine endliche Gesamtenergie. Alle Signale, die zeitbegrenzt und beschränkt sind, sind Energiesignale. Aber: auch einige zeitlich unbegrenzte Signale können Energiesignale sein!

Leistungssignale besitzen stets eine unendliche Energie. • Leistungssignale sind meist zeitlich unbegrenzte Signale. • Beispiele: x (t) = 1 oder x(t) = cos(t)
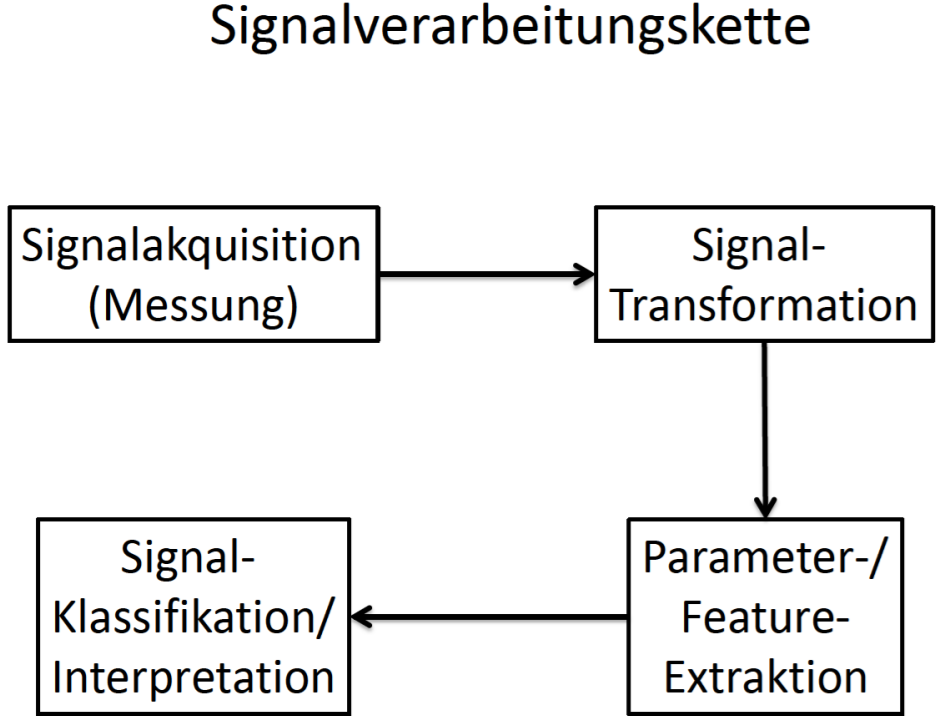
1.Signalakquisition: Erfassen des Signals mit einem Sensor und ggf. Wandlung in ein elektrisches Signal. Bsp: Biosignal
2.Signaltransformation
Ziele:
-Digitalisierung (A/D Wandlung)
-Verbesserung der Signalqualität
• Trennung von Stör- und Nutzsignal
• Reduktion der Störanteile (Artefakte), z.B. durch Abschirmung oder Filter
mögliche Störanteile: technische und biologische Artefakte (z.B.): Netzbrummen, Atmung und Bewegung im EKG, Augenbewegung und Bewegung der Gesichtsmuskeln beim EEG -> Korrektur oder Vermeidung
3. Parameter-Extraktion/Interpretation
Ziele:
1. Reduktion des Signalumfangs auf relevante Information
2. Nutzbarmachen der informationstragenden Signalteile für Signalvergleich und Signalinterpretation (z.B. Zusammenfassen, Visualisieren, statistisch auswerten)
Sprungförmige Signale: Bedeutung: • Elementare Signale zum Testen und zum Beschreiben von Systemen, z.B. zur Darstellung von Schaltvorgängen
• mathematisch gut handhabbar. Alternative Bezeichnungen: Sprungfunktionen, Impulsfunktionen, Impulse
Es gibt: Sprungfunktion • Rechteckfunktion • Rampenfunktion • Dreieckfunktion • Impulsfunktion (Dirac-Impuls)
Signaleigenschaft:
Stationarität: Um das Spektrum eines nicht-periodischen Signals zu verstehen, benötigen wir eine weitere wichtige Signaleigenschaft: die Stationarität
Bandbegrenztheit: Spektrum Bandbegrenztheit von Signalen
• weitere wichtige Signaleigenschaft
• bedeutsam bei der Digitalisierung von Signalen
• Definition mit Hilfe der Frequenz
Ein Signal x (t) heißt bandbegrenzt, wenn sein Spektrum ab einer bestimmten Grenzfrequenz fmax verschwindet.
X (f) = 0 für /f/ ≥ fmax
Bandbegrenztheit kann durch einen Tiefpassfilter erzwungen werden, der hohe Frequenzen unterdrückt!
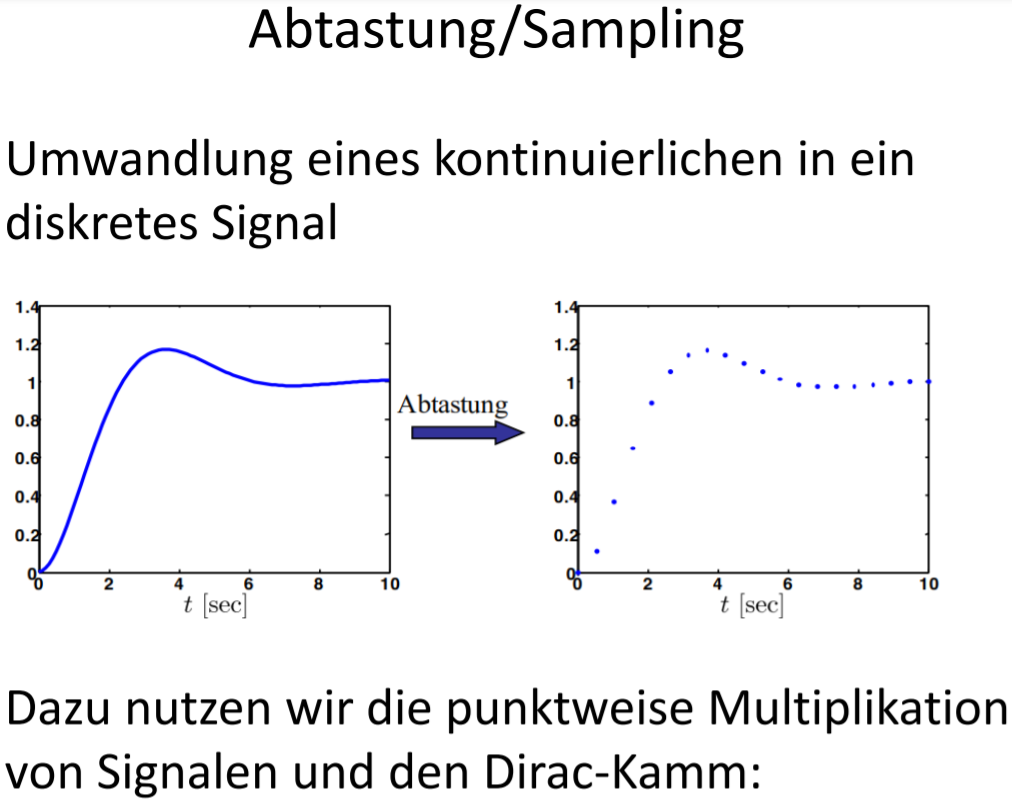
Digitalisierung
Definition: Transformation eines zeit- und wertkontinuierlichen (analogen) Signals in eine diskrete, digitale Repräsentation
Ziel: mit minimalem Informationsverlust!
2 Schritte: Abtastung (Sampling) = Diskretisierung der Zeit / Quantisierung = Diskretisierung der Signalwerte
1.Abtastung : Abtasten – Zeitdiskretisierung (bei Einhaltung des Abtasttheorems ohne Informationsverlust möglich)
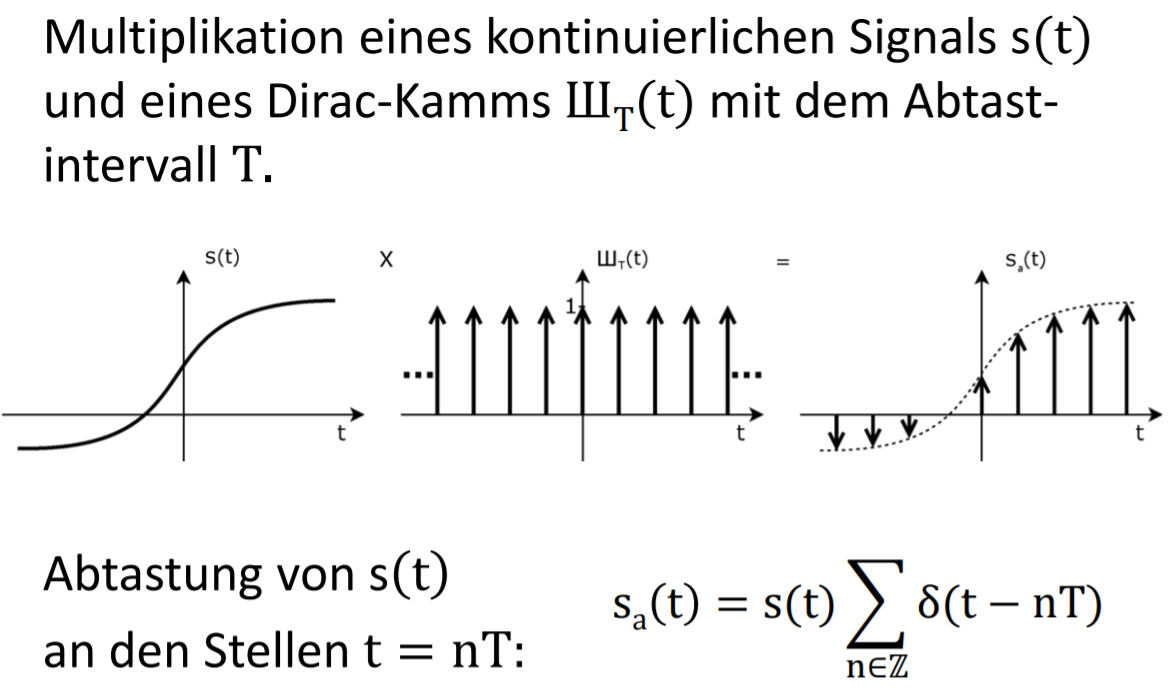

Alias-Effekt
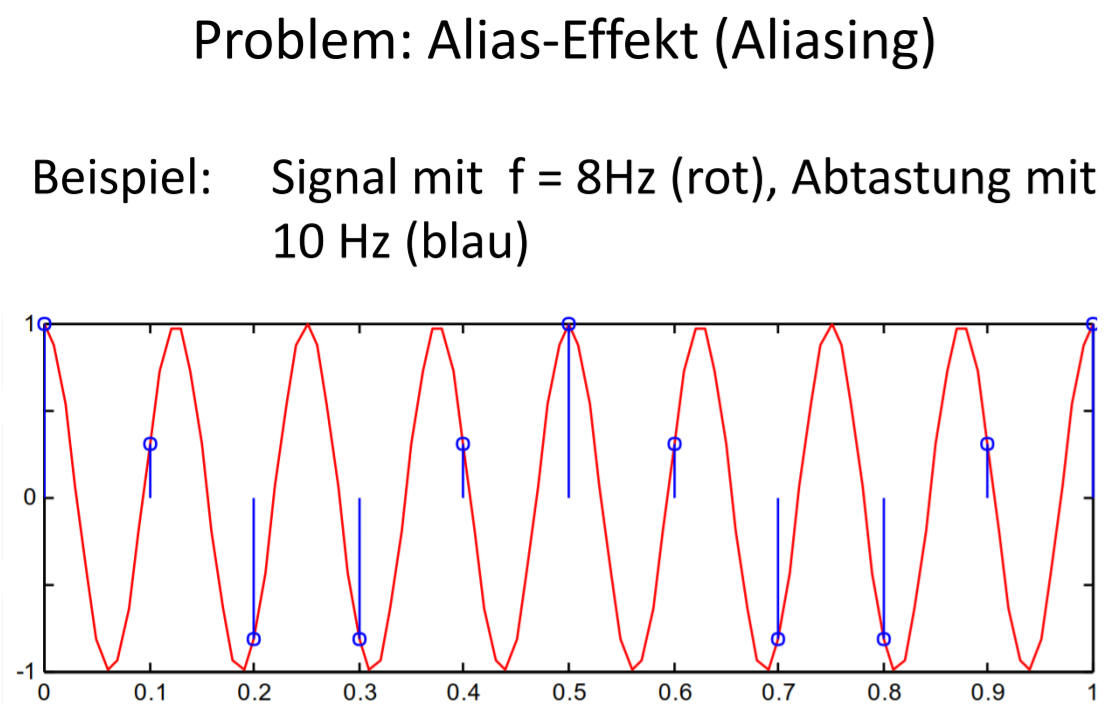
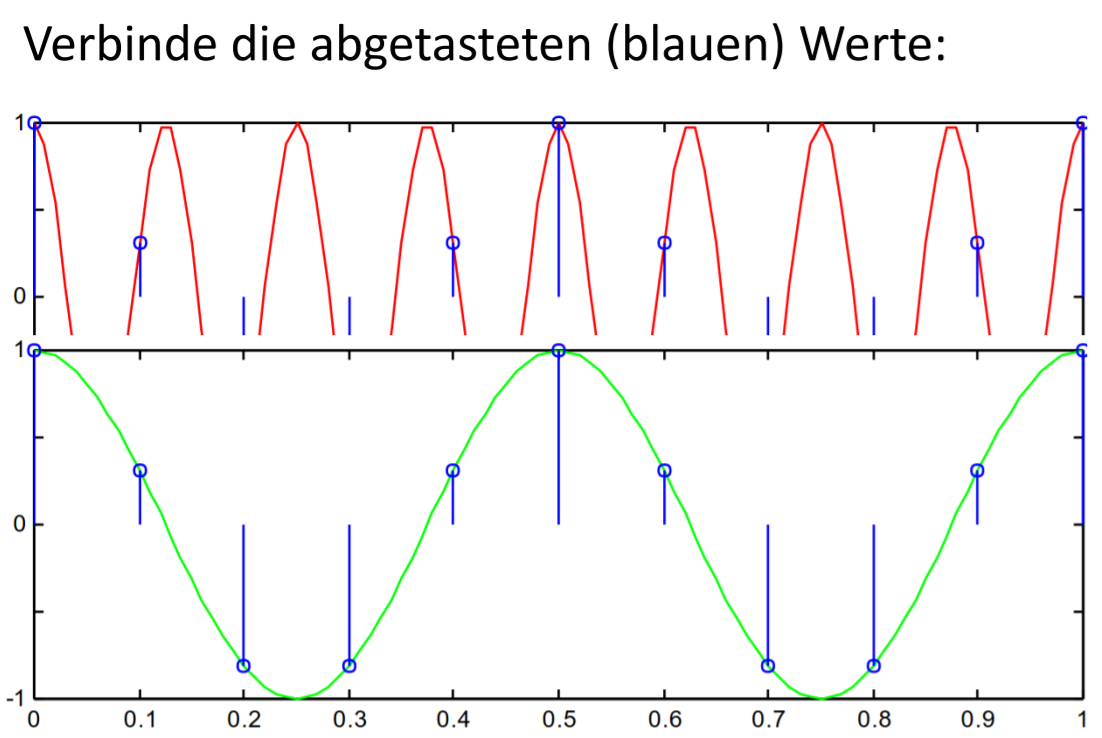
=> Es entsteht eine langsamere Frequenz, die im ursprünglichen Signal nicht enthalten war!
Dieser Effekt heißt Alias-Effekt. Er entsteht durch eine zu geringe Abtastrate!
(Um Alias-Effekt zu verhindern, können Tiefpassfilter eingesetzt werden, die unerwünschte Frequenzanteile herausfiltern.
Das Nyquist-Shannon-Abtasttheorem gibt die Frequenz an, mit der abgetastet werden muss, um keine Information zu verlieren und Alias-Effekte zu vermeiden. Die Abtastfrequenz muss mindestens doppelt so hoch sein, wie die höchste informationstragende Frequenz im kontinuierlichen Signal.)
2.Quantisierung:
Der Quantisierungsfehler ist der Fehler, der bei der Quantisierung von analogen Größen entsteht.
Während analoge Signale dem Wertebereich der reellen Zahlen genügen, werden in der digitalen Darstellung nur diskrete Werte verwendet. Daher ist mit der Quantisierung eine Rundung verbunden, die einen Fehler verursacht.


Bạn đang đọc truyện trên: AzTruyen.Top