Quelque part sur mon disque dur traînent les brouillons de PJAM. Vous avez un dossier « PJAM » qui contient une tonne de sous-dossiers et de fichiers. L'un d'entre eux est le logo du FSM et un autre une paire de lunettes « thug life ».

Gudule : aujourd'hui on raconte notre vie (je l'ai fait boire au préalable).

Et il y a aussi un petit fichier intitulé « idees.txt » dans lequel j'ai mis plein de belles idées.

Il se trouve que Maribus2000 m'a donné une meilleure idée que toutes celles qui étaient dans « idees.txt », donc je remets à plus tard le chapitre suivant que j'avais prévu.

Parlons de changements d'état en maths.

D'abord les changements d'état en physique : c'est très, très, très compliqué. Alors, ce qui est compliqué ce n'est pas de savoir que l'eau se transforme en liquide, solide ou gaz. Ce qui devient compliqué, c'est quand on demande pourquoi les changements d'état se produisent, tout simplement. Pourquoi, tout à coup, devenir solide c'est mieux. Devenir liquide c'est le top. Devenir gaz, c'est le must. Et sur ce point, je n'en sais rien. Personne n'a fait de la physique statistique ? Comment, ça ne sauve pas les meubles ?

Gudule (inspiré) : por que t'évapoooore ???

Plus amusant sur les changements d'état en physique, c'est ce genre de diagramme qu'on trace en thermodynamique : on regarde à quelles températures, et à quelles pressions les différents états existent. Surprise. Il existe un point auquel tous les états coexistent.

(Diagramme de l'eau par Maghémite sur Wikimédia commons.)

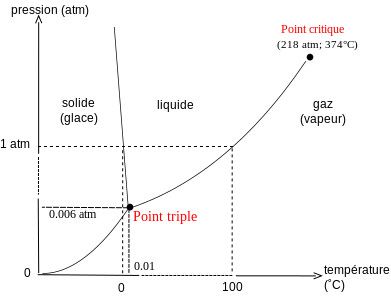
Vous savez comment fonctionne la lyophilisation ? Ça consiste à remarquer qu'il y a un autre moyen de passer de l'eau liquide à la vapeur d'eau (que ceux qui ont pensé « eau gazeuse » se dénoncent) que de chauffer comme un barbare (ce qui donnerait une sale tête aux framboises, vous voyez). Il suffit de congeler les framboises, puis de faire baisser la pression jusqu'à ce que l'eau se sublime.

Gudule : moi aussi, je...

Non.

Bref, et tant qu'on parle de ça, je pense au SF6. L'hexafluorure de soufre est un gaz facile à observer sous une forme de « fluide supercritique » (c'est ce qu'il y a au-delà du point critique sur le diagramme pression-température), parce que la pression nécessaire n'est « que » de 37 bars environ. Vous le chauffez et il finit par devenir ni liquide, ni gaz, une sorte de chose bizarre.

FTM : j'aime ça, que voulez-vous.

Gudule : et les maths, maître ?

En maths, on a des phénomènes qui ressemblent à des « changements d'états » ou « transitions de phase », comme disent les physiciens. Vous pouvez trouver des ressemblances à partir du moment où vous avez :

– une propriété observée de manière statistique sur un ensemble d'objets

– qui dépend de certains paramètres et change brutalement en fonction de ces paramètres

Gudule : les exemples.

Un exemple amusant : la « satisfiability threshold conjecture » (conjecture de l'échelon de satisfiabilité, en français ce n'est pas plus clair).

L'histoire porte sur des formules logiques propositionnelles. Du genre : (A et non B) ou C , etc. La grande quête des informaticiens est de se donner une telle formule et de savoir si elle est satisfiable ou non, autrement dit, si en donnant certaines valeurs « vrai » ou « faux » aux variables (A, B, C... ) qui sont impliqués, on va arriver à :

VRAI.

Par exemple si A est vrai, B est faux, (A et non B) est vrai, donc c'est satisfiable. Exemple assez ridicule, je suis d'accord. En revanche (A et non A) n'est pas satisfiable. Trouver les meilleurs algorithmes de satisfiabilité et les optimiser est un domaine de recherche en soi, et c'est utile au monde réel (celui des avions et des microprocesseurs). Mais c'est compliqué.

Vous construisez maintenant des formules en forme normale conjonctive, donc en gros :

C1 ET C2 ET ... ET Cn

Où C1, C2, ... Cn sont des « clauses » qui sont elles-mêmes des « OU » de variables (les A, B, C... ) ou de leurs négations (NON A, NON B, ... ).

La conjecture dont on parle ici dit que : si vous construisez des formules comme ça, au hasard, avec des clauses d'une certaine taille k, et que vous gardez constant r, le nombre de clauses sur le nombre de variables, vous avez :

Conjecture : il existe une certaine constante rk telle que, à r constant, si la taille de la formule croît, sa probabilité d'être satisfiable tend vers :

– 0 si r > rk (en d'autres termes, vous avez trop de contraintes sur les variables)

– 1 si r < rk (vous avez beaucoup de variables et peu de contraintes, ça « peut » donc être vrai)

(Ça a juste été démontré pour le cas k=2, ce sont donc des formules logiques construites de manière très simple.)

La « transition de phase », le « changement d'état », se produit donc lorsque r = rk. À ma connaissance, on a utilisé dans l'étude de cette transition des outils mathématiques connus de la physique statistique (mais cela, vous vous en doutez, dépasse mes compétences). D'où le lien avec les changements d'état en physique !

Plus terre-à-terre peut-être, une source astronomique d'exemples de ce genre est aussi l'étude des graphes aléatoires.

Les informaticiens étudient des graphes provenant du monde réel (réseaux sociaux, pages web, fanbase de Gudule...). Ces graphes peuvent par exemple être modélisés avec des propriétés telles que : deux sommets quelconques ont une probabilité p d'être liés entre eux (mais ce modèle-ci est un peu trop simple, on en a beaucoup d'autres).

L'étude des graphes aléatoires va donc vous dire des choses intéressantes sur les graphes du monde réel. Mathématiquement, ce sont des outils simples de probas (sinon, je me serais enfui) appliqués aux graphes.

Imaginez que vous avez un graphe aléatoire à n sommets, sur le modèle de : deux sommets quelconques sont liés avec probabilité p. Si p est une constante, votre graphe est « asymptotiquement » (quand n devient grand) « presque toujours connexe », c'est-à-dire qu'il y a un chemin entre chaque paire de sommets. Donc p constante, c'est trop fort. Vous le faites varier en tant que fonction de n. Vous observez alors des changements d'état :

– au début, p=0, tout le monde est seul dans son coin.

Gudule : où sont mes fans ?

– à p = 1 / n², la première arête apparaît.

Premier fan de Gudule : hey, salut, tu veux lire ma chronique ?

Gudule : euh, vote d'abord.

– de petites composants apparaissent, pas très grosses.

Gros fan de Gudule : Gudule ! Gudule ! Gudule ! Je partage tes ouvrages avec tous mes abonnés. Nous allons conquérir le monde !

Fan de Norbert : je suis un fan de Norbert.

Autre fan de Norbert : moi aussi.

– une « grosse composante connexe » finit par apparaître. Celles qui restent sont peu nombreuses, de taille proportionnelle à ln(n) en moyenne (oui, ln, le logarithme népérien, le fameux, celui qui croît moins vite qu'un escargot senior asthmatique).

Gudule : mes fans ! Je vous aime !

Fans de Gudule : quand est-ce qu'on a le prochain chapitre ?

Fans de Norbert : on n'est pas nombreux, mais on préfère Norbert.

– finalement lorsque p = ln(n) / n, vous passez de « non-connexe presque tout le temps » à « connexe presque tout le temps ».

Gudule : le monde est tout entier constitué de mes fans ! (admirez cet alexandrin fortuit)

Norbert : ouin, je suis mon seul follower... s'il vous plaît... en désespoir de cause, je mets des photos de chatons (et bientôt Harry S.).

Vous avez de tels échelons pour l'apparition de triangles dans votre graphe, par exemple, ou toute autre propriété qui vous amuse.

Un des rares cas dans lesquels je me suis retrouvé à faire des probas.

Gudule : et quelques mois plus tard, il s'est mis à écrire PJAM. Une coïncidence ? Je ne crois pas.