Vers le XVIe siècle, les mathématiciens se jetaient des défis consistant à résoudre des équations polynomiales.

Une équation polynomiale, donc, c'est quand vous cherchez les X tels que P(X) = 0, où P est une expression polynomiale plus ou moins moche. Par exemple X² - 2 = 0.

Les solutions ? parfois, il y en a, parfois, il y en a pas. Parfois on a de belles formules, parfois c'est compliqué (c'est plutôt exceptionnel d'avoir des formules, il faut le dire).

Il se trouve qu'un dénommé Tartaglia (c'étaient des italiens) avait trouvé une formule intéressante en 1535, déjà découverte avant par quelqu'un d'autre et gardée jalousement secrète (je vous rassure, garder des résultats secrets ça ne se fait plus aujourd'hui). Il se trouve que pour trouver cette formule, une façon de faire consiste à passer par des racines carrées de nombres négatifs, des nombres « imaginaires ».

Heureusement, ils disparaissaient tous à la fin, mais ces formules étaient donc, on peut le dire, marquées d'un sceau démoniaque.

Tartaglia : c'est bizarre, mais ça marche.

FTM : tiens, un autre de mes adorateurs. Salut.

Mais nous sommes en maths. Tous les nombres sont déjà imaginaires. Et il est tout à fait possible de définir les nombres complexes, comme une extension des réels, et de les munir de leurs opérations.

Par exemple, il suffit de dire que les complexes sont des couples de réels et que lorsqu'on les multiplie entre eux, on fait « comme si » (a,b) était en fait (a + bi) où i est la racine carrée de -1.

Gudule : mouais.

Les complexes ont la plupart des avantages des réels (pas de problème sur les opérations), et ils ont un pouvoir extraordinaire en plus : ils sont algébriquement clos.

Gudule : gné.

L'idée de clôture algébrique est la suivante : on part des réels et on s'intéresse aux équations polynomiales. Par exemple, X² = -2.

Gudule : pas de solution dans les réels.

Exactement. Une clôture algébrique des réels, c'est un ensemble, plus gros, dans lequel toutes ces équations ont une solution et où tu les retrouves. Et qui est lui-même « clos », c'est-à-dire que toutes ces équations y ont une solution. On aime donc les complexes pour cette propriété fondamentale et souvent utile.

En revanche, il n'y a pas de notion de « signe » et d'ordre dans les complexes. Pas de complexes « positifs » et « négatifs », ça n'a pas de sens et certaines propriétés des réels sautent.

Alors, une fois appris ce que sont les complexes, les enfants demandent :

Gudule : qu'est-ce qu'il y a au-delà ?

Eh oui, jusqu'où peut-on définir des « nombres » ?

Au-delà, il y a des tonnes de structures plus ou moins jolies. Mais rien – RIEN où on retrouve les propriétés habituelles des opérations. Par exemple, on peut construire les quaternions, qui sont un genre de super-complexes ; au lieu d'être de dimension 2 (a + bi), ils sont de dimension 4 (a + bi + cj + dk) et la multiplication n'y est plus commutative : dans un produit, l'ordre a une importance.

Ils sont utiles en mécanique spatiale, cependant. On peut les utiliser pour représenter des rotations.

Gudule : et au-delà ?

Et on peut encore aller plus loin ! On obtient les octonions, à huit dimensions. Cette fois ils n'ont même plus l'associativité de la multiplication. Ça veut dire que (a fois b) fois c et a fois (b fois c) ne sont pas la même chose.

Gudule : et au-delà ?

Eh bien, les sédénions ! 16 dimensions ! Et on perd encore des propriétés. Par exemple, il peut exister deux nombres non nuls dont le produit est 0 ! Tu es content de toi, Gudule ?

Gudule : meh...

On peut poursuivre ce genre de construction à l'infini, mais on n'a plus grand-chose qui ressemble à un nombre.

Pour résumer, un petit schéma de Gudule (c'est censé ressembler à un dessin du système solaire, avec des orbites toujours plus éloignées).

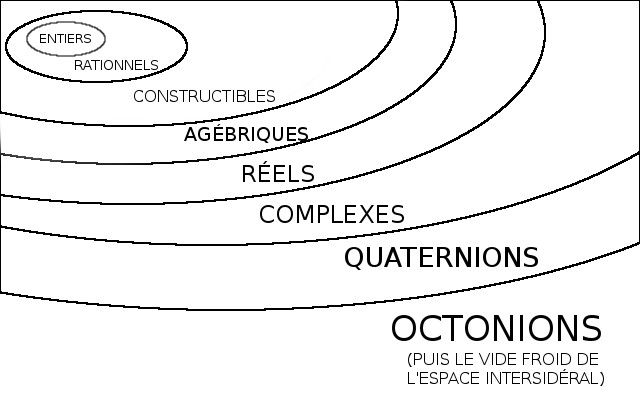
Vous aussi vous trouvez qu'il s'améliore ? (il faut le dire, c'est important de le valoriser)