Sitôt que nous avons en main les nombres entiers, nous ressentons une envie irrépressible.

Gudule : fuir.

Non, Gudule, nous avons envie de les décomposer.

Les matheux font ça avec tout ce qui leur passe sous la main : on décompose et on reconstruit. Ça permet de comprendre le comportement des objets. En particulier l'étude des structures en algèbre consiste souvent à décomposer ces objets et les reconstruire à partir de petits bouts (groupes, espaces vectoriels, algèbres, monoïdes, modules, semigroupes, etc.). Et parfois c'est simple (espaces vectoriels de dimension finie, un monde merveilleux plein de licornes roses invisibles), parfois c'est compliqué (classification des groupes simples finis... mouhahahahaha ! À suivre.)

Eh bien vous savez quoi ? Pour assister à des problèmes de décomposition parmi les plus ardus, les nombres entiers suffisent.

Gudule : comment voulez-vous décomposer, maître ?

Bien sûr, décomposer les nombres avec l'addition, on a compris que c'était plutôt simple.

Gudule : 3 = 1 + 1 + 1

Ouais, super.

Mais tentons maintenant de faire ça avec la multiplication.

Gudule : 4 = 2 fois 2, 6 = 2 fois 3, et 7 égale, euh... 7 fois 1.

Haha.

Donc, oui, il existe des entiers particuliers que vous ne pouvez pas écrire comme le produit de deux entiers différents tous deux de 1 : ils sont indécomposables. Ils sont premiers. Ils ont un nom qui fait peur.

Et un coup d'œil aux nombres premiers suffit pour être témoin de problèmes qui ont des répercussions assez nombreuses dans le reste des mathématiques. Comme une onde à la surface de l'eau qui grandit, grandit, et fait une grande vague emportant Gudule sur son passage.

Quelques remarques qui se démontrent : les nombres premiers existent en infinité et chaque entier se décompose de manière unique en produit de nombres premiers (ce n'est pas évident, mais ça se fait). Et maintenant, le théorème de Gudule :

Théorème de Gudule : les nombres premiers sont placés en vrac.

FTM : alors, justement, j'avais prévu de les espacer correctement mais je venais d'inventer le beurre et j'ai glissé. Eh, c'est pas de ma faute, on m'a donné 7 jours pour finir le monde, et je n'ai même pas de bras.

Alors, dire qu'ils sont placés « en vrac » n'est pas tout à fait vrai. Des calculs savants permettent de rendre compte de la densité du nombre de nombre premiers. En gros, si vous prenez un nombre x au hasard, la probabilité qu'il soit premier est 1/ln(x) , où ln est... euh... le logarithme népérien, une chose qu'on rencontre en Terminale S (j'en parlerai forcément dans ces pages). Ceci aussi se démontre, avec moult raffinements, des approximations toujours plus subtiles. Retenons juste que : 1. ils sont en infinité, mais en grandissant, on en trouve de moins en moins, 2. POURQUOI ? POURQUOI LE LOGARITHME ? On aura tout vu.

Théorème de Gudule : les nombres premiers ne sont pas tout à fait placés en vrac, mais en regardant de près, c'est le vrac.

Vérifiez : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37

Et non, 1 n'est pas premier. Il est malheureux.

Au départ je pensais que c'était assez méchant de réduire les nombres premiers à cette seule remarque dramatique, mais dans la pratique, c'est quand même le nœud du problème. Bien sûr, on peut démontrer plein de choses marrantes avec les nombres premiers, par exemple : tout nombre premier de la forme 4k + 1 est la somme de deux carrés d'entiers. Vérifiez avec 5 = 4 + 1, 17 = 16 + 1, 29 = 25 + 4, etc.

Gudule : on comprend donc assez bien le comportement des nombres premiers.

FTM : hem...

C'est ça, c'est ça, on comprend bien. Maintenant jouons à un jeu, Gudule : prends un nombre pair, et trouve-moi deux nombres premiers dont il est la somme.

Gudule : 16 = 11 + 5

Si ça te dit, tu peux vérifier aussi loin que les capacités de calcul des ordinateurs actuels le permettent, une telle décomposition va toujours exister. Mieux, tu vas même en trouver plein. Et donc :

Conjecture (Goldbach) : tout nombre pair plus grand que 2 est la somme de deux nombres premiers.

Tout est dit. Ce qui est marrant avec ce problème, c'est qu'il est vieux (XVIIIe siècle). Et comme tout problème très vieux qui dure depuis très longtemps, il tient parce qu'il y a un très gros os à ronger : les propriétés additives des nombres premiers. Tout le reste, c'est de la blague à côté, parce que le résultat a une saveur "multiplicative" (je creuserai un peu tout ça un jour).

Il y a quelque temps je me posais la question : tout ça ne vient-il pas juste de la répartition des nombres premiers ? Oui, le coup fumeux du logarithme. Alors allons-y, prenons au hasard des « faux » nombres premiers, ayant exactement la même répartition. J'ai bien dit au hasard, avec une belle fonction random() dans Python (si tant est que ce soit vraiment du hasard... supposons que oui). Je les sélectionne, il y en a autant que les « vrais » et ils se placent à peu près pareil.

Voici le résultat. Je trace : en axe horizontal, le nombre pair que je décompose, en axe vertical le nombre de décompositions qu'il a. Pour les deux je suis allé jusqu'à 10 000, une bagatelle.

D'abord les faux, ensuite les vrais.

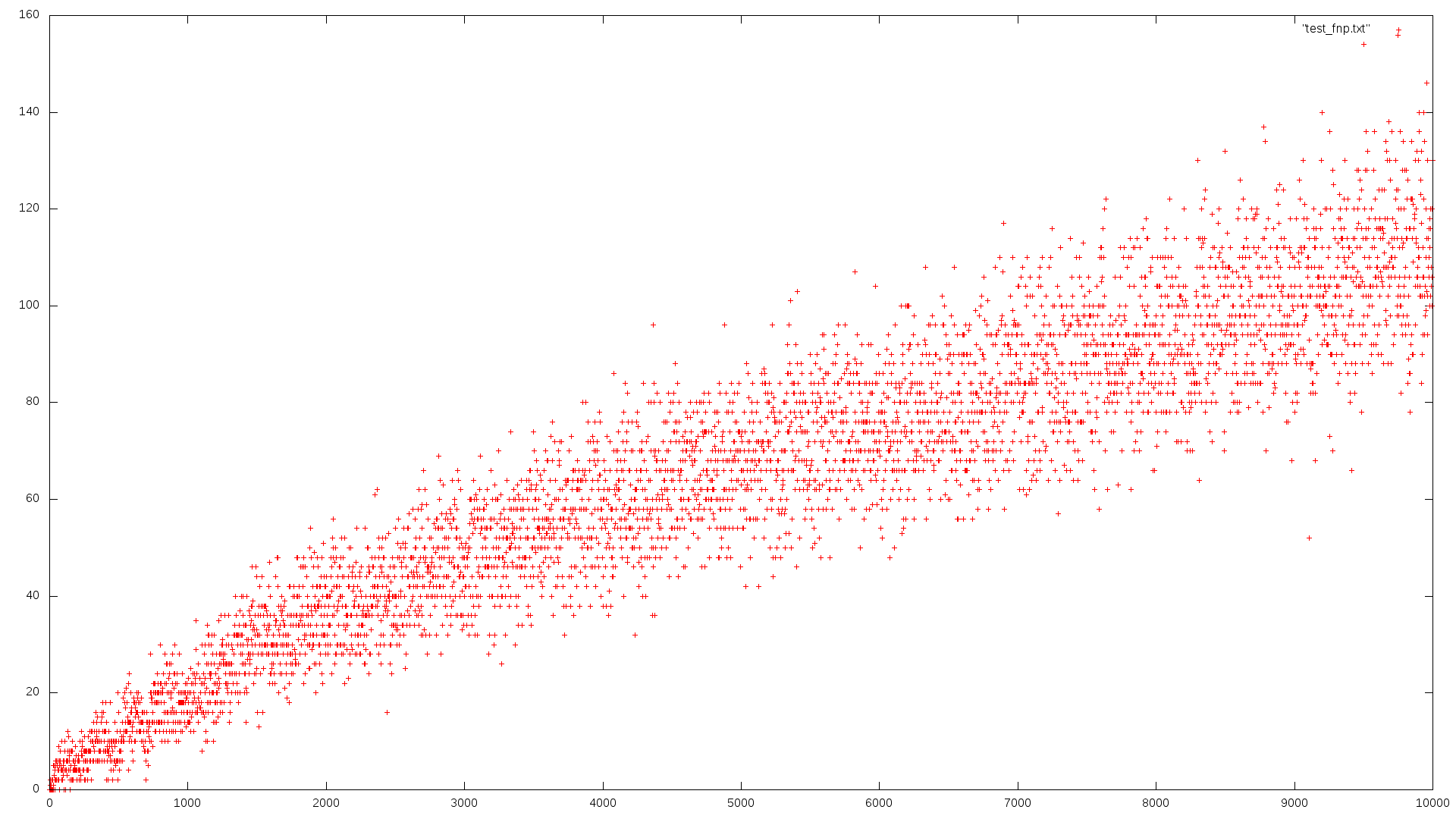
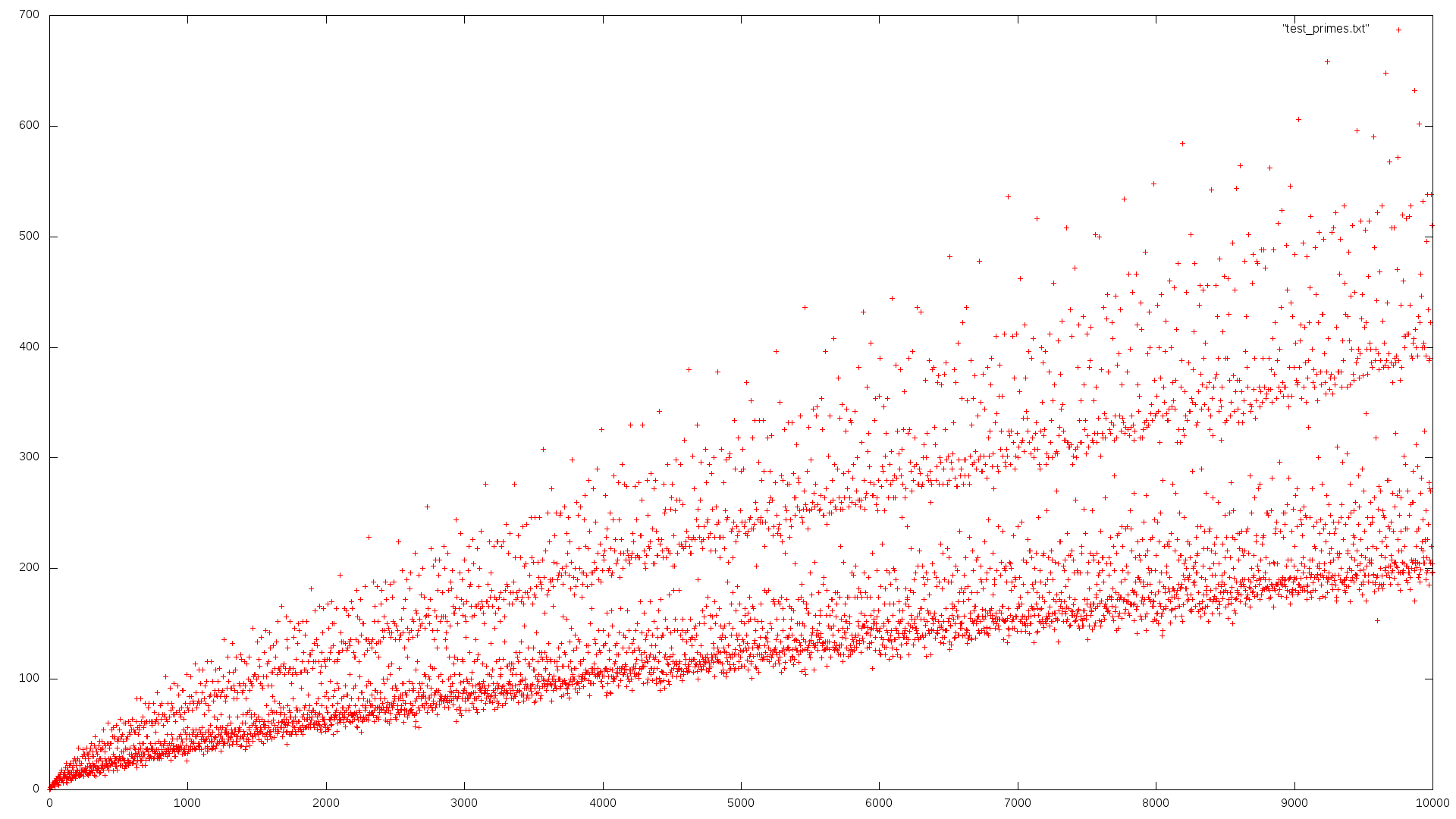
Surprise ! Pour les vrais premiers, ça monte jusqu'à 700, pour les faux, jusqu'à 160.

Gudule : maître, ça ne marche pas. Il y a beaucoup plus de décompositions pour les « vrais » nombres premiers que pour les « faux ».

Taisons-nous et admirons sur le deuxième graphique la comète de Goldbach.

Oui, elle est en couverture de ce bouquin. La comète de Goldbach, c'est cette étrange répartition du « nombre de décompositions en somme de deux nombres premiers ». Qui dessine de superbes faisceaux, comme une queue de comète (les matheux sont des poètes). Je n'ai jamais trouvé le moindre petit début de bout d'explication sur cette répartition (pas que je me souvienne). Sachant que les matheux préfèrent déjà sans doute chercher à démontrer que les décompositions existent.

Vous avez bien suivi. On voit désespérément sur ce graphique que même pour les plus malchanceux, le nombre de décompositions trouvées devient de plus en plus grand (l'infini n'est pas loin). Et on ne sait toujours pas démontrer qu'il y en a au moins une pour chaque. Un jour j'ai dit ça à des collégiens et ils faisaient cette tête :

À moins qu'ils aient juste eu peur de ma coiffure.

Voilà pourquoi j'adore l'arithmétique.

Petite précision pour terminer : en l'état actuel, il semblerait qu'une version faible de la conjecture de Goldbach ait été démontrée en 2013 : tout entier impair > 5 est somme de trois nombres premiers. Pas mal, non ? Je pense être incapable de comprendre comment ça marche sans deux mois de temps libre et une dizaine de litres de café. Et un deuxième assistant.

-------------------------------

C'est bizarre ? C'est trop long ? C'est trop court ? Les graphiques sont moches ? Vous n'aimez pas l'arithmétique ? Vous êtes tristes qu'on n'ait pas parlé de produits laitiers ? Le Monstre Tortellini Volant se fera une joie de répondre à vos commentaires avant même qu'ils soient postés.

Pour le reste, l'inspiration divine m'a fait commencer un peu vite mais le rythme de publication va se calmer un peu, bien qu'une foule de choses se pressent. Dès le théorème de Gödel passé, ce ne sera plus qu'une croisière d'agrément.

D'ailleurs, si vous avez des questions ou un super futur sujet, lâchez-vous, on (je ?) va encore bien s'amuser !