Nous devons à Benoît Mandelbrot (1924-2010), un grand mathématicien de la génération post-Seconde Guerre Mondiale, d'avoir donné un nom à la notion de fractale. Il n'existe en réalité pas de véritable définition mathématique universelle pour ce concept. En tant qu'objet géométrique, une fractale est un dessin ou un solide pourvu d'autosimilarité, avec des motifs qui se répètent à l'infini – souvent d'une très grande complexité. Quand vous zoomez sur une fractale, vous retrouvez tout ou partie de la fractale elle-même.

Dans le monde réel, il s'agit d'un objet qui a cette caractéristique de complexité et d'autosimilarité, mais bien sûr, pas à l'infini : c'est donc plutôt une approximation. Par exemple, certains flocons de neige, le dessin de la côte norvégienne, ou le chou Romanesco.

FTM : pour les besoins de cette expérience, nous avons transformé Gudule en chou Romanesco, mais rassurez-vous, il parle toujours.

Gudule : je me sens extrêmement déprimé.

C'est pour la science, Gudule. Dis-nous ce que tu ressens dans cette nouvelle forme.

Gudule (motivation équivalente à celle d'un crustacé) : je suis fractal.

C'est bon, Gudule, arrête de rouler partout.

Gudule (cri de désespoir) : je suis un chou fractal !

Si vous êtes un chou, il n'est pas absurde de pousser en adoptant une structure récursive, chaque petit bout ressemblant à nouveau au tout. On imagine très bien un bourgeon qui donne naissance à d'autres bourgeons identiques, etc., le tout se répétant à l'infini.

FTM : ou sinon, vous pouvez considérer que le chou Romanesco est ainsi parce que je l'ai décidé... afin que l'homme aie l'idée d'inventer les fractales ! Tout est lié, voyez-vous. Je n'ai rien fait au hasard.

Crédit pour le chou : Coyau / Wikimedia Commons / CC-BY-SA-3.0.

Au départ je voulais visualiser des fractales avec un programme maison, mais finalement j'ai eu la flemme et Gudule programme trop mal. Donc je prends XaoS. Vous aussi pouvez télécharger et utiliser XaoS pour visualiser et zoomer sur des fractales. Ça amuse pendant quelques heures, après il faut quand même trouver autre chose à faire de sa vie (travailler, par exemple).

J'ouvre le « Readme » donné avec le code source. Dans les remerciements figurent Newton, Mandelbrot, Richard M. Stallman, Linus Torvalds. Et il y a une section « non-remerciements » où figure Bill Gates tout seul.

Gudule : LOL.

Un logiciel fait pour me plaire.

Bon, avant toute chose il faut savoir ce qu'est un nombre complexe. Gudule, les complexes en 20 mots.

Gudule : un nombre complexe, c'est a + bi où a et b sont des réels, et i est « la chose ».

Les mathématiciens se sont écharpés pendant des décennies sur la question de ce qu'étaient les nombres complexes. En effet, i est « le nombre qui au carré, vaut -1 », et quant à savoir s'il a le droit d'exister... mais il est bien possible de définir ces nombres. Et comme nous sommes en maths, tant qu'on peut définir quelque chose, ça existe.

Gudule : c'est l'explication des nombres complexes la plus bâclée que j'aie jamais vu. On reprendra ça dans un prochain chapitre.

En particulier, les matheux aiment à regarder le plan, là où vous faites de la géométrie depuis tout petit, comme strictement équivalent aux nombres complexes (a + bi, deux coordonnées, le monde est bien fait). Autant je déteste la géométrie, autant j'aime l'analyse complexe.

Gudule : bon, mais quel rapport avec les fractales ?

On peut définir les fractales à partir de certaines suites de nombres complexes. Par exemple pour l'ensemble de Mandelbrot.

Prenez un nombre complexe c et définissez une suite de nombres complexes qui commence à 0, et où chaque nombre suivant est obtenu en mettant le précédent au carré et ajoutant c. Selon la valeur de c, cette suite va avoir un comportement différent :

– elle va grossir indéfiniment ;

– ou pas.

Quand ça ne part pas vers l'infini (et au-delà), c est dans l'ensemble de Mandelbrot. Sinon, il n'y est pas.

Cette définition est très simple (si, si, c'est élémentaire), mais elle suffit à obtenir un ensemble extrêmement bizarre, comme vous le savez sans doute. Les autres fractales usuelles ont des définitions similaires. Pour faire plaisir aux yeux, zoomons sur l'ensemble du Phénix. Cette fois la suite est z(n+1) = z(n)² + Re(c) + Im(c)*z(n-1). Re(c) et Im(c) sont les deux « coordonnées » du nombre complexe c (détail que vous êtes autorisés à oublier).

Gudule : d'où viennent les couleurs ?

Alors, les couleurs ne sont pas là que pour faire joli, elles sont obtenues en regardant le comportement de la fameuse suite. Si ça part vers zéro, si ça oscille, etc. Je dois dire que je n'en sais pas plus, j'ai surtout sélectionné la colorisation la moins moche. Gudule, envoie les images et commente.

Gudule : première image, les ailes du phénix.

Gudule : deuxième image, zoom sur une aile du phénix.

Gudule : troisième image, on s'approche de la spirale.

Gudule : image 4 : on plonge dans la spirale.

Gudule : image 5 : on plonge encore.

Gudule : image 6 : on arrive sur les îles du bord de la spirale.

Gudule : le zoom sur ces îles révèle de complexes entrelacs bleus spiralés.

Gudule : dernière image : on s'arrête sur le rivage de l'atoll.

Merci, Gudule. Qui de mieux qu'un chou fractal pour commenter les fractales ?

Gudule : justement, j'ai une réclamation à faire sur mon statut actuel. Je vais créer un syndicat.

Il existe une deuxième façon d'obtenir des fractales. Cette fois, ça consiste à se balader sur le plan en sautant de façon aléatoire. Mais le seul exemple que j'ai retrouvé est le triangle de Sierpinski. Le voici, obtenu avec Python en traçant 15 000 points de la façon suivante :

– partir de x=0.5, y=0

– à chaque tour, prendre le milieu entre le point actuel et un des trois sommets du triangle, pris au hasard avec même probabilité.

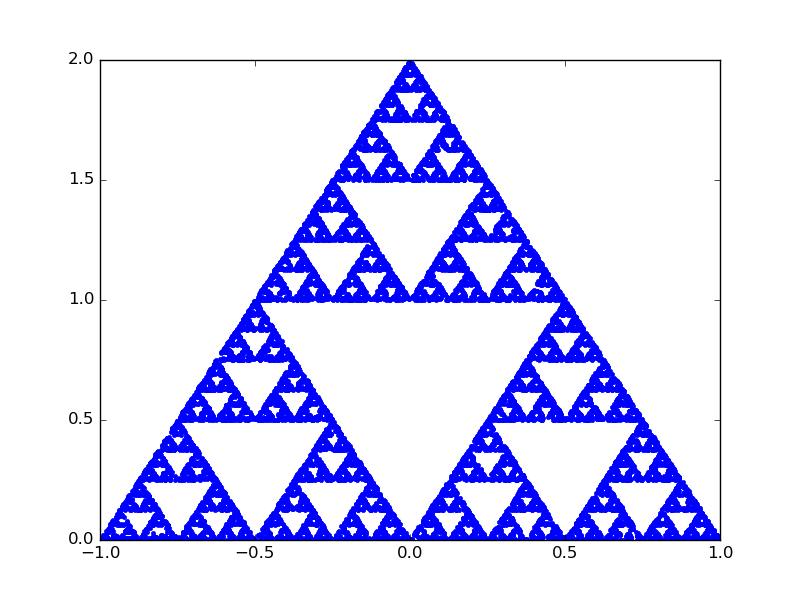
Que devons-nous retenir ? Bah, c'est beau. En plus de ça, les fractales telles que Mandelbrot les a popularisées sont les objets par excellence pour :

– avoir une description simple (trois lignes, ma définition des suites complexes, c'est ridicule !)

– et malgré tout, avoir une structure compliquée

Bien sûr, c'est utile pour générer des décors de jeux vidéos réalistes (des montagnes, des arbres, etc.), mais les figures sont déjà superbes en soi. Il y a beaucoup à dire sur le sujet, mais je suis plutôt ignorant, ce segment n'était là que pour mettre enfin de jolies images dans ce bouquin... et introduire les nombres complexes en 5 lignes. Parce que je compte en parler de nouveau plus tard.