Felice anniversario della nascita di Karl Weierstrass!

Chi? Ma come, chi?

Weierstrass, Karl Theodor Wilhelm Weierstraß, il padre dell'analisi matematica moderna!

Si occupò di molti ambiti, ma soprattutto dei fondamenti dell'analisi, e fu diede contributi che ancora oggi portano il suo nome: il Teorema di Weierstrass sui massimi e i minimi, il Teorema di Bolzano-Weierstrass sulle successioni limitate e il criterio di Weierstrass per la convergenza uniforme delle serie di funzioni. Dimostrò l'esistenza di una funzione continua, ma non differenziabile in nessun punto, ovvero, che non può essere mai derivata. Inoltre, la definizione di limite che usiamo tutt'oggi è quella che venne ideata da Weierstrass: la sua nuova formulazione permise di eliminare le ambiguità presenti nel concetto intuitivo di limite come era stato pensato da Leibniz, Newton, Euler e i Bernoulli.

Questi studi miravano a portare chiarezza nell'analisi, in modo da evitare clamorosi errori commessi dai suoi predecessori e ragionamenti intuitivi del tutto errati...

Cosa, non vi interessa? È noioso?!?

Ah, ma forse vi aspettavate altro?

Giusto, comprendo: siete giunti qui attirati dal titolo.

La casa degli orrori matematici, o dovrei forse dire "errori"?

In effetti, pare il tema giusto per la notte di Samhain, che gli anglosassoni chiamano Halloween.

Bene, allora, venite avanti. Seguitemi oltre questa soglia, prego, ma state in guardia: questa piccola collezione di orridi errori e conclusioni mostruose potrebbe sconvolgervi e farvi dubitare di tutto!

Qui non si parlerà di semplici sbagli, come ad esempio scrivere + al posto di - e viceversa, o perdere un fattore 2 passando da un'uguaglianza ad un'altra. Sono conscio del fatto che questi errori mietono fin troppe vittime nel tetro campo di battaglia delle verifiche e dei compiti scolastici e universitari.

Eppure, questi non sono certo orrori interessanti, dato che sono dovuti alla pura distrazione, e possono capitare a tutti.

Non parleremo neanche di dimostrazioni errate di enunciati veri. Questa altra classe di errori comprende tutte le strade sbagliate e insensate che dovrebbero portare un'affermazione corretta.

Facciamo comunque un esempio per capire come possano essere. Per dimostrare la formula

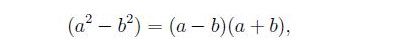
(ovvero, la regola della somma per la differenza), consideriamo il rapporto

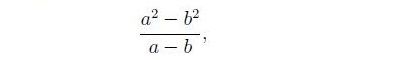
e "cancelliamo" un a e un b, e poi "semplifichiamo" - al numeratore con - al denominatore ottenendo +, 

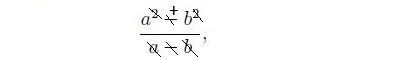
ossia a + b; come volevasi dimostrare.

Il ragionamento è palesemente insensato, e ignora le più basilari regole sulle somme e le divisioni. Tuttavia, non è veramente temibile: i passaggi assurdi sono sotto gli occhi di tutti, e difficilmente può trarre in inganno.

Infine, ci sono gli errori veri e propri, quelli che andremo ad affrontare, ossia ragionamenti apparentemente corretti, che però contengono una più o meno sottile falla logica, e che portano a risultati assurdi o sbagliati, i quali però sembrano convincenti in forza della "dimostrazione".

1 = 2 : un grande classico!

Non potevo esimermi dal cominciare con questa perla di assurdo.

Dunque, siano a, b numeri reali, e si supponga che 

a = b. 

Se moltiplichiamo entrambi i lati dell'uguaglianza per a, otteniamo

Ora sottraiamo b^2 da entrambi i membri e ricaviamo

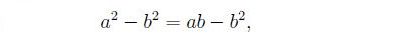
che si può fattorizzare in 

(a - b)(a + b) = b (a - b).

Adesso dividiamo per (a - b), e quindi otteniamo 

 a + b = b, 

ma a = b, e quindi 2a = a. 

Ora, la scelta iniziale di a era arbitraria, perciò possiamo scegliere a = 1, e otteniamo quindi 1 = 2!

In effetti, da 1 = 2 segue subito che 0 = 1, il classico risultato che fa capire che i conti precedenti devono per forza contenere un qualche errore fatale.

Forse i più smaliziati tra voi avranno già trovato l'imbroglio, ma lascio un piccolo indizio agli altri: siamo sicuri che potessi dividere?

π è un numero intero: tutti quei decimali sono un complotto della lobby degli irrazionalisti!

(Qui incollerò l'immagine della pseudodimostrazione per intero, perché Wattpad non può reggere troppe immagini, dovrebbe essere leggibile.)

Riuscite a capire dove sta l'inghippo o dovremo concludere che pi greco sia uguale a 3?

Indizio: occhio all'estrazione delle radici quadrate!

1 metro è uguale a 1 centimetro: questa farà impazzire chi di voi ha avuto problemi con le equivalenze!

Si ha che 1 m = 100 cm, e quindi ne segue che 

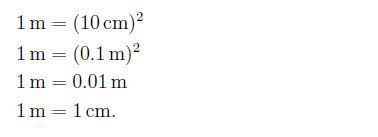
Accidenti, che disdetta! Pare proprio che il sistema metrico decimale sia da buttar via dalla finestra!

Oppure no? 

1 = 0, stavolta lo dimostriamo usando le serie infinite!

Mi rendo conto che molti di voi non hanno mai sentito parlare delle serie infinite. Si tratta di un argomento estremamente affascinante dell'analisi matematica, e pure Weierstrass se ne occupò a lungo.

In poche parole, una serie è una somma di infiniti addendi numerici. Facciamo un esempio, per aiutarvi a capire: possiamo sommare

1 +  1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ...

e andiamo avanti all'infinito, aggiungendo gli inversi di tutte le potenze di 2. Si può dimostrare che, contrariamente a quello che si potrebbe pensare, questa somma di infiniti termini non dà infinito, ma 2. Per provarlo, poniamo

P = 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + ...

e osserviamo che, moltiplicando per 2, si ottiene

2 P = 2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + ... = 2 + S.

Dunque, ne segue che 

2 P = P + 2, 

ovvero, P = 2.

Incredibile, vero? Oppure vi pare chiaro e semplice?

Come che sia, questo risultato è vero, e potete verificarlo usando la vostra calcolatrice, se volete: andando avanti a sommare gli inversi delle potenze di 2, vedrete che la somma si avvicinerà sempre di più a 2.

Ebbene, bisogna stare attenti: non tutte le operazioni usuali delle somme valgono, quando si sommano infiniti addendi.

Passiamo quindi al prossimo assurdo: sia

S = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ...

ovvero, sommiamo 1 e -1 infinite volte. Ora, possiamo raggruppare le infinite coppie di 1 e -1, ottenendo

S = (1 - 1) + (1 - 1) + (1 - 1) + (1 - 1) + ... = 0 + 0 + 0 + 0 + ... = 0.

Tuttavia, possiamo anche lasciare il primo 1 da parte e poi raggruppare le infinite coppie di - 1 e 1:

S = 1 + (- 1 + 1) + (- 1 + 1) + (-1 + 1) + (-1 + 1) + ... = 1 + 0 + 0 + 0 + 0 + ... = 1.

Dunque, poiché si tratta sempre della serie S, dobbiamo concludere che 1 = 0.

Stavolta vi ho già lasciato intendere dove sta il problema: non possiamo raccogliere i termini e cambiare l'ordine della somma come preferiamo, quando andiamo a sommare infiniti numeri!

Arriviamo ora all'ultimo pezzo di questa piccola esposizione. Se ancora la vostra mente non è stata scossa da quanto avete già letto, credo che questo vi colpirà, o nulla affatto saprà mai stupirvi!  

+ ∞ = - 1: l'infinito è un numero negativo! Nulla ha senso!

Ehehe, mi sono tenuto la parte migliore per il finale.

Anche stavolta avremo bisogno di impiegare le serie infinite.

Sia

G = 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + ...

ovvero, sommiamo tutte le potenze di 2: badate bene, non stiamo prendendo gli inversi, ma le potenze con esponente positivo.

Pare chiaro che 

G = + ∞. 

Insomma, stiamo sommando infiniti numeri sempre più grandi, è ovvio, no?

Proviamo a fare come prima e moltiplichiamo tutta la somma per 2:

2 G = 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + ... = G - 1,

perché 1 non compare più nella somma, giusto?

Allora, basta risolvere

2G = G - 1

per ottenere

G = -1.

E quindi, l'infinito positivo coincide con - 1!

Ma non è finita qua, oh, no!

Se moltiplichiamo per - 1, troviamo che l'infinito negativo coincide con 1: - ∞ =  1! 

E moltiplicando l'infinito positivo per se stesso otteniamo ancora 1, perché - 1 per - 1 fa 1: 

(+ ∞)*(+ ∞ ) = + ∞ = (-1)*(-1) = 1! 

Quindi l'infinito positivo è anche uguale a 1!

Ne segue immediatamente che tutti i numeri interi sono infiniti, perché si costruiscono usando 1 e - 1!

Ma allora tutti i numeri finiti sono in realtà infiniti!!!

https://youtu.be/4O5dwh9FKqw

Muhahaha!!

Direi che per stasera abbiamo fatto abbastanza danni, meglio fermarci veramente qui. 

Spero che abbiate gradito.

Felice Halloween!

PS: Alcuni degli esempi che vi ho mostrato sono stati presi dai libri Fallacies in Mathematics, di E. A. Maxwell, e Gli errori nelle dimostrazioni matematiche, di Giorgio Balzarotti e Pier Paolo Lava.

PPS: Giusto per non lasciare in sospeso il discorso su Weierstrass, voglio raccontarvi qualche altro fatto interessante su di lui.

Weierstrass studiò matematica da autodidatta, perché il padre voleva imporgli una carriera da funzionario governativo. Di conseguenza, non si laureò regolarmente e soffrì perfino di alcolismo, a causa dei conflitti con il padre e per la frustrazione che provava. Furono le fruttuose ricerche matematiche che conduceva nel tempo libero a salvarlo dalla dipendenza. In seguito, ottenne un dottorato honoris causa e una cattedra di professore, per i risultati di enorme importanza che aveva conseguito.

Inoltre, fra i suoi illustri allievi ci fu una delle pochissime donne matematiche del diciannovesimo secolo, ovvero Sof'ja Kovalevskaja, che ho già citato nell'ultima challenge. Weierstrass accettò di darle lezioni private, poiché le donne non erano ammesse all'università di Berlino, dove lui era professore, e ne riconobbe il grande talento.

Se volete saperne di più, potete leggere la raccolta di biografie I grandi matematici, di Eric T. Bell.