Salutations chers élèves ! Vous avez vu les bases concernant les fonctions dans le chapitre précédent, il est donc temps d'aller plus loin ! Il existe une infinité de fonctions différentes, pourtant certaines formes reviennent assez souvent, et ce sont celles-ci que nous allons voir aujourd'hui.

Niveau : 3e - 2nde

----------------------------------------

Dans tout ce chapitre, la lettre x désignera l'inconnue, donc la donnée qu'on fait varier pour observer sa transformation par la fonction étudiée. La lettre f désignera la fonction elle-même, et les lettres a, b et c désigneront des constantes, donc des nombres fixes (on les note avec une lettre parce que savoir quel nombre c'est n'a pas d'importance, ça fonctionne pour n'importe quelle valeur tant qu'elle ne change pas une fois qu'on l'a choisie).

Fonction constante

C'est la plus basique des fonctions : elle ne change pas par rapport à l'inconnue.

Sa formule est de la forme : f(x) = a.

Exemple pour a = 5 : f(x) = 5.

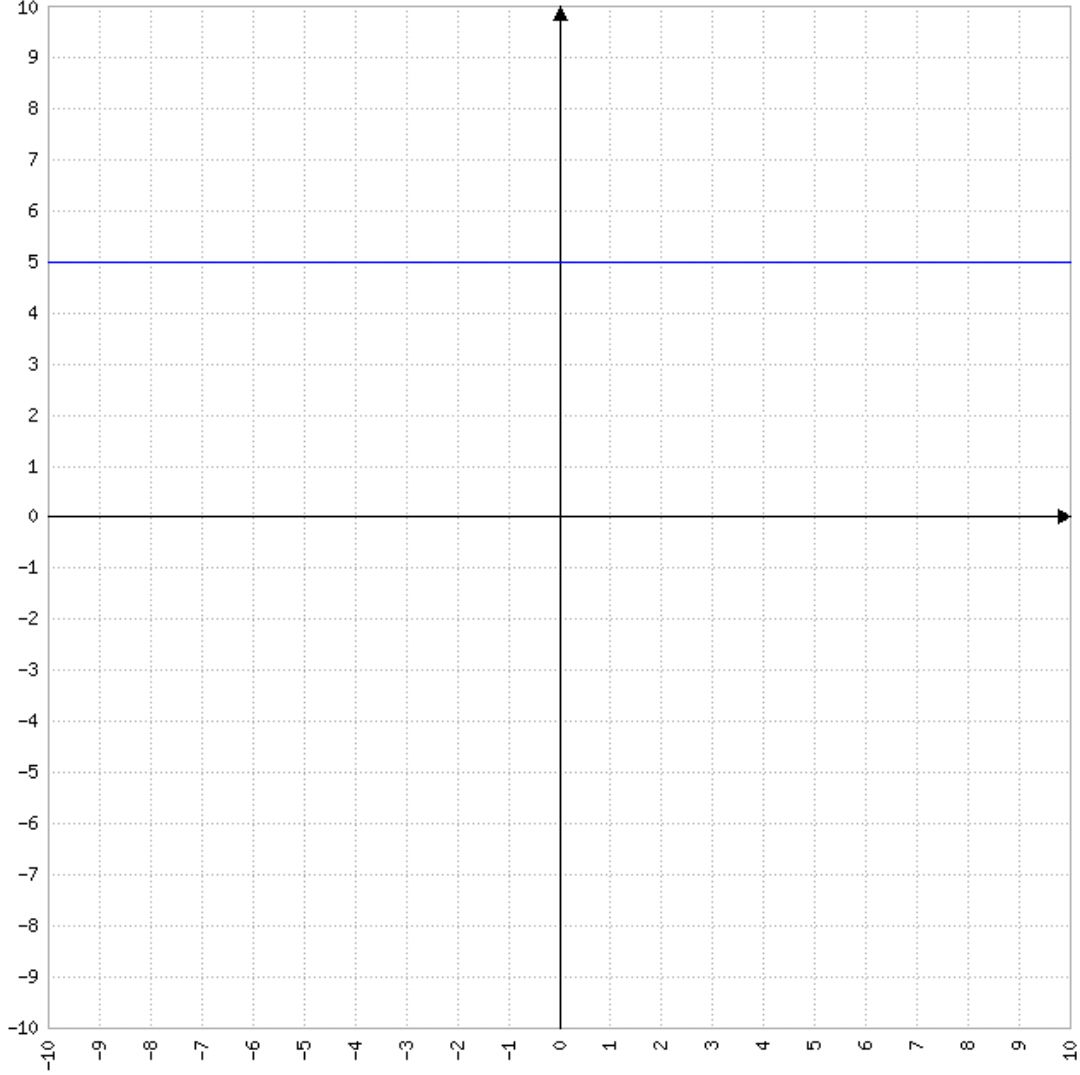
Facile non ?

Fonction linéaire

Sa formule est de la forme : f(x) = ax.

Exemple : f(x)= 3x.

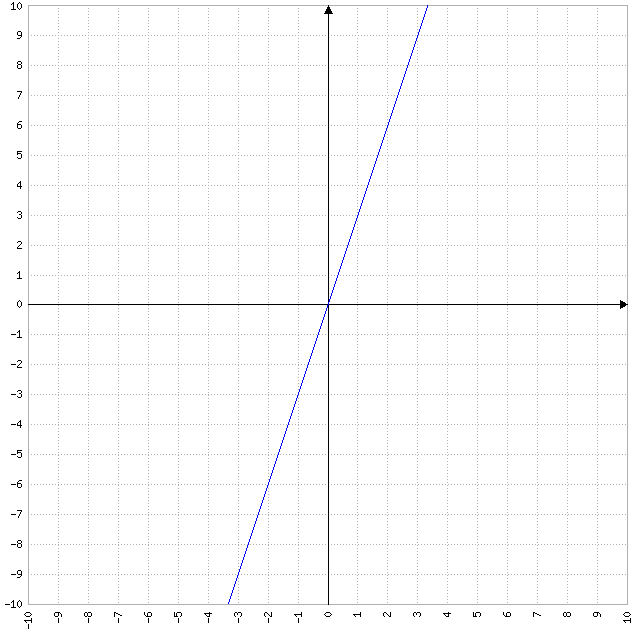
C'est juste une ligne droite, mais pas horizontale. Les images sont directement proportionnelles à leur unique antécédent, et la droite passe par l'origine du repère, à savoir le point (0,0).

Fonction affine

Elle se présente sous la forme : f(x)= ax+b.

Exemple : f(x) = 3x+2.

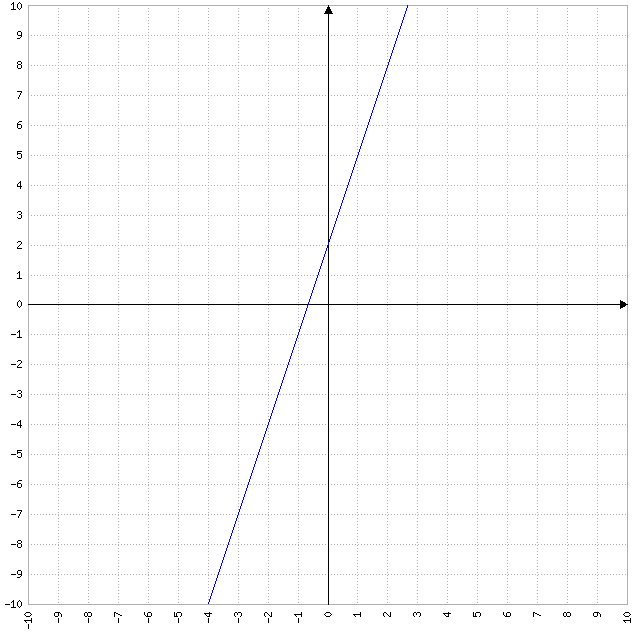
La courbe est droite mais ne passe pas par l'origine. En fait, elle est décalée vers le haut ou le bas en fonction de b. Elle passera toujours par le point (0,b).

Pour les fonctions linéaires et affines, la droite monte quand a est positif et descend quand a est négatif. a est appelé le coefficient directeur car il indique la direction de la courbe. De plus, si vous avez bien compris la notion de coefficient directeur, vous aurez également compris que la fonction constante n'est qu'une fonction affine dont le coefficient directeur est égal à zéro. f(x) = 5 peut également se noter f(x) = 0x+5

La parabole

Une courbe plus spéciale : elle se représente sous la forme : f(x) = ax²+bx+c. Sur cet exemple, qui est le même que dans le chapitre précédent, on prend a = 1, b = 0 et c= 0, ce qui donne f(x) = x².

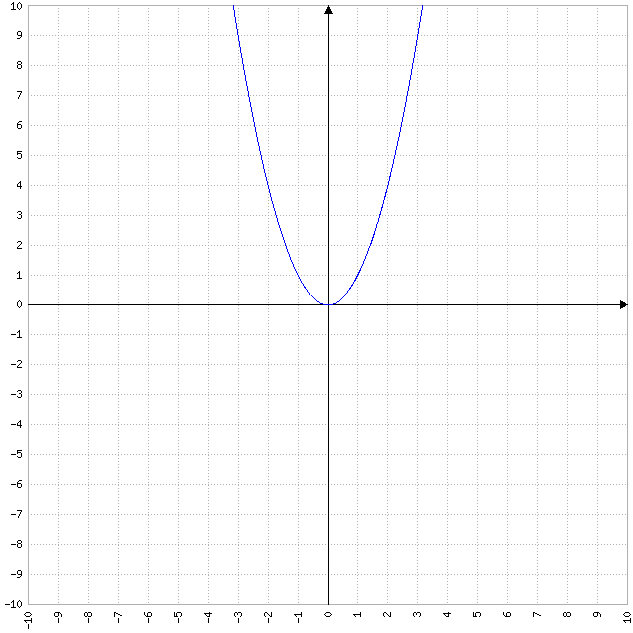
La parabole est tournée vers le haut si a est positif, et vers le bas si a est négatif.

Elle est symétrique en une droite verticale. Le point d'intersection entre cette droite et la courbe s'appelle le sommet. Sur la courbe d'exemple, l'axe de symétrie est l'axe des ordonnées et le sommet est le point (0,0).

L'hyperbole ou fonction inverse

C'est une courbe assez spéciale qui descend en se rapprochant de 0 quand x grandit vers l'infini et fait des sursauts vers l'infini quand x se rapproche de 0. Et quand je dis l'infini, ça peut être l'infini positif ou l'infini négatif.

Voici une représentation pour vous aider à comprendre.

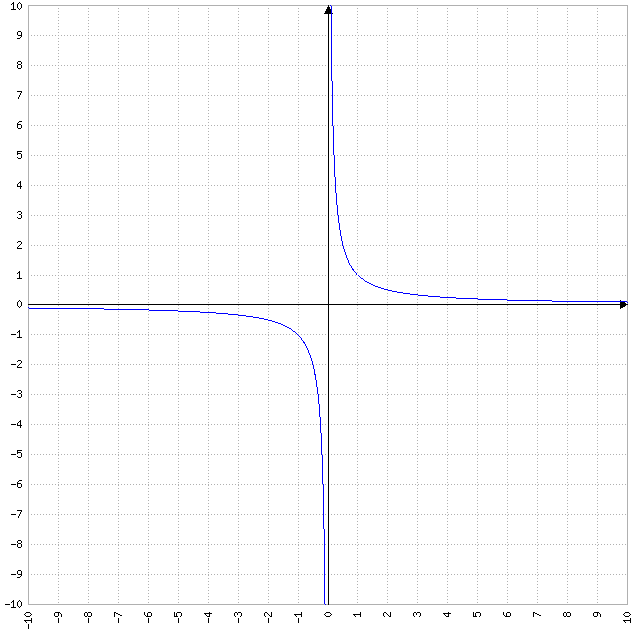
Elle se définit sous la forme : f(x) = (a/x) + b. Sur la courbe exemple, on a pris le cas le plus simple : f(x) = 1/x.

f(0) n'existe pas puisque le dénominateur d'une fraction ne peut pas être égal à 0.

Voilà, c'est tout pour les différents types de fonctions ! Gardez en tête qu'il en existe bien d'autres mais ce ne sont que les plus communes !

N'hésitez pas à poser des questions en commentaires si vous en ressentez le besoin =}

----------------------------------------

Ce cours a été rédigé par Corblanc et complété par AshenKer !