Bonjour, bonsoir, et bienvenue dans ce cours de maths proposé par Roukika ! Il me semble qu'on voit tout ça en sixième, mais je ne suis plus vraiment sûre... En tout cas, c'est un cours qu'on utilisera très souvent en maths.

Je pense que c'est tout de même important de savoir qui est ce cher Pythagore. Parce que c'est bien beau d'utiliser son théorème, mais si on ne sait pas qui l'a inventé, c'est moins intéressant.

Bref, Pythagore, il est né près d'Athènes, au Vème (5ème) siècle avant Jésus Christ. À part inventer un théorème, il a fait d'autres choses, il était notamment philosophe. Si vous savez d'où il vient et de quand c'est déjà pas mal.

Donc ce qu'on va étudier aujourd'hui date d'il y a 2500 ans... Oui, c'est très vieux ! 

Le théorème de Pythagore s'utilise dans un triangle rectangle. Si vous n'avez pas de triangle rectangle, vous ne pourrez pas utiliser le théorème ! Ensuite, ce cher théorème va nous permettre de trouver la longueur d'un des côtés du triangle, si on connait les deux autres. Il pourra aussi, par la suite, nous aider à prouver si un triangle est rectangle ou non, grâce à la réciproque du théorème, mais ne vous inquiétez pas, je réexpliquerai ça un peu mieux quand on y sera.

Propriété 1 : le théorème de Pythagore dit : "Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égale à la somme des carrés des longueurs des côtés de l'angle droit".

Bon, quand on lit ça comme ça, on n'y comprend pas grand chose. 

D'abord, est-ce que tout le monde se souvient de "l'hypoténuse" et des "côtés de l'angle droit" ? Si vous ne comprenez pas, aller voir le cours précédent sur la trigonométrie, c'est expliqué dedans.

Ensuite, on peut aussi bloquer sur le mot "carré". Lorsqu'on met un nombre "au carré", ça signifie qu'on va le multiplier par lui-même. On le note "²", et on le place juste après le nombre qu'on veut mettre au carré. Par exemple : 2² = 2x2 = 4 et 5² = 5x5 = 25. Vous avez compris ? On ferra sûrement un autre cours sur les puissances pour mieux expliquer tout ça.

Maintenant, si on traduit cette propriété sous forme d'une égalité, voilà ce que ça donne :

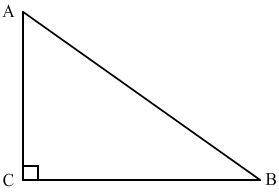
AB² = AC² + BC². (Le triangle juste au-dessus, c'est pour savoir où sont les lettres A, B et C.)

Rien de bien compliqué jusque là ? On va faire un petit exemple :

Voici comment on m'a appris à rédiger pour utiliser le théorème :

Le triangle TRS est rectangle en R,

J'utilise le théorème de Pythagore.

TS² = RT² + RS²

TS² = 3²+4²

TS² = 9+16

TS² = 25

TS = *racine carrée de* 25

TS = 5.

Vous suivez ? Ah, mais il y a le mot "racine carrée" qui vous bloque ? C'est simple, c'est l'inverse de l'opération "au carré". Voilà la notation :

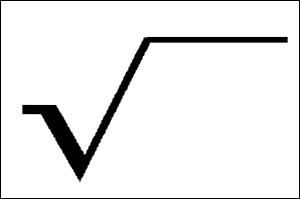
C'est un espèce de "v" où on monte le deuxième trait, qu'on prolonge un peu, comme pour faire un "toit". Sous ce toit, on inscrit le nombre à qui on veut trouver la racine carrée. Un petit exemple ? *Racine carrée de* 25 = 5 / *Racine carrée de* 36 = 6 / *Racine carrée de* 4 = 2. Un autre cours expliquera un peu mieux tout ça, bien-sûr.

Bref, revenons à notre théorème. Là, on a trouvé la manière de connaître la valeur de l'hypoténuse. Mais quand on veut trouver un des côtés de l'angle droit ? Voici un autre petit exemple :

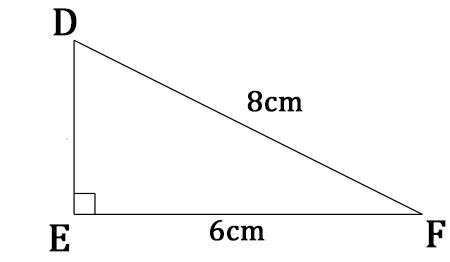
Le triangle DEF est rectangle en E,

J'utilise le théorème de Pythagore.

DF² = EF² + DE²

8² = 6² + DE²

64 = 36 + DE²

64 - 36 = DE²

DE² = 64 - 36

DE² = 28

DE = *racine carrée de* 28

DE ≈ 5,29.

Apprenez juste cette méthode par cœur, on apprendra les équations un autre jour, et là vous comprendrez (ça fait beaucoup de cours à écrire tout ça !).

Voilà, maintenant vous savez utiliser le théorème de Pythagore, il ne reste plus qu'à apprendre la réciproque du théorème de Pythagore. Hepepep ! On reste gentiment à sa place jusqu'à la sonnerie ! Je vous vois déjà quitter cette page au plus vite, mais c'est pas encore fini ! Bientôt, je vous promet.

Une propriété réciproque, en gros, c'est l'inverse de la propriété de base.

Propriété 2 : la réciproque du théorème de Pythagore dit : "Si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et son hypoténuse est le plus grand côté".

Voilà ce que ça nous donne de manière simplifiée :

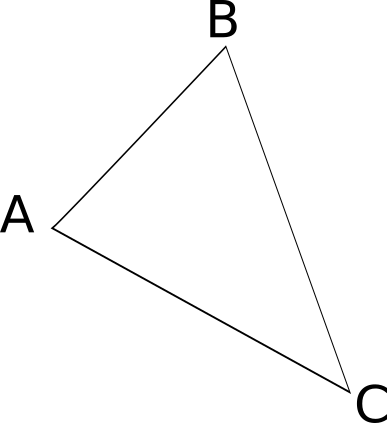
Si BC² = AC² + AB², alors ABC est rectangle en A.

On mettra toujours la valeur du plus grand côté à la place de BC.

Exemple : (ici aussi, c'est la méthode qu'on m'a apprise pour utiliser la propriété).

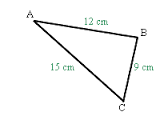
Dans le triangle ABC, le plus grand côté est AC.

AC² = 15² = 225.

AB² + BC² = 12² + 9² = 144 + 81 = 225.

On constate que AC² = AB² + BC².

J'utilise la réciproque du théorème de Pythagore.

Donc ABC est un triangle rectangle en B.

Pour finir, si l'égalité est fausse, on va utiliser la contraposée de la réciproque du théorème de Pythagore.

Propriété 3 : Si, dans un triangle ABC (avec AB le plus grand côté), AB² ≠ AC² + BC², alors le triangle n'est pas rectangle.

Exemple :

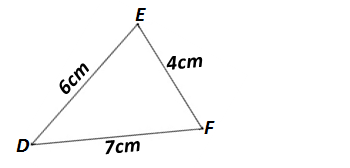
Dans le triangle DEF, le plus grand côté est DF.

DF² = 7² = 49.

DE² + EF² = 6² + 4² = 36 + 16 = 52.

On constate que DF² ≠ DE² + EF².

J'utilise la contraposée du théorème de Pythagore.

Donc le triangle DEF n'est pas rectangle.

Voilà, enfin la fin de ce long cours. J'espère que vous aurez tout compris, mais je pense qu'une grande partie connaissait déjà le théorème de Pythagore. Si vous avez des questions, n'hésitez pas !

À bientôt !