Heya ! Bienvenue dans le cours de maths de Urachi-Ember ! Aujourd'hui, je vais vous faire un cours de troisième sur la trigonométrie ! C'est parti !

Bon, je vais vous donner les définitions, puis après les astuces et le reste !

La trigonométrie est la partie des mathématiques qui établit un lien entre les mesures des angles des triangles rectangles et les longueurs de leurs côtés (enfin en tout cas, c'est la première des utilisations qu'on en fait).

Les formules de trigonométrie permettent :

1. De calculer les longueurs des deux autres côtés d'un triangle rectangle lorsqu'on connaît la longueur d'un côté et les mesures d'au moins deux angles.

2. De calculer les mesures des deux angles autres que l'angle droit si on connaît les longueurs d'au moins deux côtés.

Normalement, en quatrième vous avez déjà vu la formule du cosinus d'un angle qui est (longueur adjacent) / (longueur hypoténuse).

Rappel : Les côtés d'un triangle peuvent être qualifiés d'adjacents, hypoténuse ou opposé.

• L'hypoténuse est le plus grand côté d'un triangle rectangle.

• Le côté adjacent à un angle est le côté qui touche cet angle mais qui n'est pas l'hypoténuse.

• Le côté opposé à un angle est le côté qui ne touche pas cet angle.

Généralement, on galère à retenir les formules de Cosinus, sinus et tangente, qui sont respectivement cos = Adjacent/Hypoténuse, sin = Opposé/Hypoténuse et tan = Opposé/Adjacent

Retenez juste ça : CAHSOHTOA

Si tu comprends pas ce que ça veut dire, si ton prof de maths t'énerve, lui dis pas "casse-toi", c'est une mauvaise idée. Bref, après cette blague pourrie je vais expliquer la formule

CAH veut dire Cosinus Adjacent Hypoténuse

Donc Cosinus est égal au côté adjacent divisé par l'hypoténuse

SOH = Sinus Opposé Hypoténuse

TOA = Tangente Opposé Adjacent

Allez, petit exercice pour vérifier si vous avez compris, et pour reprendre la formule de ma collègue Lina_love_leopardus, ON NE COPIE PAS !

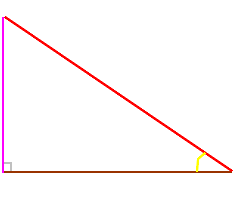
Par rapport à l'angle jaune, à quoi correspondent les côtés rouge, rose et marron ?

Allez, autre exercice, sur les formules cette fois !

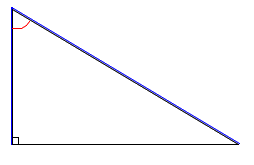
On connaît les longueurs bleues, on cherche l'angle en rouge, quelle formule on doit utiliser ?

Bon, aussi, après avoir la mesure d'un angle en connaissant son cosinus , il vous suffit d'utiliser la touche "arccos" sur la calculatrice, puis d'écrire le cosinus et ensuite fermer la parenthèse !

Pareil pour sinus avec arcsin, et pour tangente avec arctan.

Bon, sur le triangle précédent, si l'hypoténuse mesure 6 centimètres et le côté adjacent en mesure 3, combien de degrés mesure l'angle ?

Bon, dernière phase, calculer une longueur si on a un angle et une longueur !

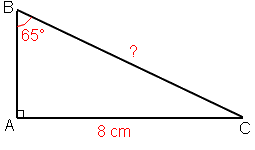
1. On cherche l'hypoténuse et on connaît le côté opposé. On utilise donc la formule du sinus.

2. sin(ABC) = AC/BC

3. sin(65) = 8/BC

4. BC * sin(65) = 8

5. BC = 8/sin(65)  

Donc BC ≈ 8,8cm.

Voilà, si tu as compris, je te demande de faire cet exercice, si tu n'as pas compris, relis donc ! :)

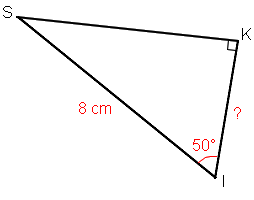
Donne un arrondi à 0,1cm près de la longueur KI

Allez, je vous laisse, j'ai des copies à corriger !