9. HOW TO READ MINDS
1. color clairvoyance
The performer proves (by magician's logic) that he can distinguish between colors without seeing them.
Display several wax crayons of the sort that children use with coloring books. "Magic," you begin, "is sometimes very useful. When I'm driving my car I never need to look at a traffic light to know whether it is red, yellow, or green. I just guess — and I'm always right. 'll show you."
Put your hands behind your back, and turn away from the audience. "Select one of the crayons and give it to me behind my back." When this has been done, face the audience again.
Behind your back, dig the nail of the middle finger of your right hand into the end of the crayon and scrape off a small piece of the colored wax. Bring this hand to the front, place it against your forehead, and concentrate. If you keep the fingers curled inward as your hand moves up to your forehead, you can spot the particle of crayon under the fingernail, and note its color.
Don't name the color immediately; that makes it look too easy. Pretend that what you are doing is difficult, and that you really are receiving faint mental impressions. Also, as should be done in most mind-reading tricks, give the information out piecemeal. "I get the impression of a light color... yellow, perhaps, or orange . . . I feel it more clearly now... the color is yellow!" This adds suspense and is dramatically effective.
Finally, prove that the trick wasn't just a lucky guess by doing it again once or twice.
2. Seeing with the finger tips
Several colored objects are given to the magician behind his back and he apparently distinguishes one color from another by touch.
Any small, differently colored objects may be used — crayons, pencils, swizzle sticks, soda straws. In advance, push about four such objects, crayons, let us say, under the band of your wrist watch and up along the inner side of your arm (fig. 43). Memorize the order of the colors from left to right.

figure 43
Begin the trick by handing out four duplicates. "I can," you announce, "tell one color from another by sense of touch alone. I can see color with my finger tips. Mix these colored crayons and then hand them to me behind my back."
After this has been done, face the audience again. Behind your back place the crayons in your hip pocket. Ask someone to name one of the colors. Immediately pull the crayon of the proper color from the memorized group that you have hidden up your sleeve, and toss it out.
Then produce the remaining colors, as called for. Do this rapidly; the faster it is done, the more difficult it seems to be.
3. magic arithmetic
A spectator is given a pad and pencil and asked to write down any number of three different figures. Then he is to reverse this number (for example: 673 reversed gives 376) and subtract the smaller number from the larger.
In most problems of this sort the performer, given the final answer, names the original number. But here, apparently knowing nothing at all, he concentrates and gives the answer.
Stand away from the spectator so that you can't see what is written but keep an eye on the movements of the spectator's pencil.
The answer usually contains three figures; occasionally only two. It is easy to tell by watching the pencil when the spectator writes a two-figure answer. You always know immediately what this is because a two-figure answer is always
In a three-figure answer, the middle digit is always 9, and the two outside digits always add up to 9. You have two chances to get the information you need. It is easier than you think to recognize the number being written by watching the pencil. If you get either the first or last number, you know the other number. For example, if 2 is the first number written (in subtracting, the answer is written from right to left) the three-digit answer must be 792.
Don't announce the whole number. Ask the spectator to concentrate first on the first digit of the answer. Do this even though you may have failed to recognize the number from the pencil movements.
Then name the first digit. If necessary, just make a guess.
If you are correct, the trick is as good as done because you know what the other two numbers must be. If you have made an error, or are simply guessing and are wrong, accuse the spectator of not concentrating hard enough, and ask for the number.
"Let's take the second digit, and please concentrate on it hard. I can't get any thought waves unless you broadcast a few"
This time you are correct; the second digit is always 9.
Since you now know the first digit, subtracting it from 9 gives you the third digit. Even if you fail on the first digit, your ability to pull the rest of the answer out of thin air is impressive.
After having done this two or three times so that the spectators realize that different answers are obtained, throw in this variation. Any number of three different figures is reversed, and the smaller subtracted from the larger as before.
Then the answer is reversed, and this new figure added.
Example:
845
— 548
297
+792
1,089
This time you can keep your back turned during the whole trick, and get every digit of the answer every time. This procedure always gives an answer of 1,089.
4. numbers in the mind
There are several mathematical tricks in which the performer discovers a mentally-selected number after the spectator has performed some calculations with it and announced his result. This trick is much more mystifying. The spectator begins with an unknown number, and the performer gives the final answer without knowing the original number and without asking any questions.
Ask someone to think of a number and then pretend to concentrate. "Ninety-five thousand, seven hundred and sixtytwo. No! Not such a big number, please. That is much too difficult. Less than ten, please. Good. That's much better."
Then tell him to make the following calculations:
Double the number,
Add 8,
Divide by 2,
Subtract the original number.
"Now concentrate on your answer. You are thinking . . . of the number .. . four!"
This will be correct because the answer is always half the number you told him to add, in this instance, 8. Example:
6 X 2 = 12 + 8 = 20 + 2 = 10 - 6 = 4.
Now, before anyone has time to think about it and realize that the answer may always come out the same, do it again. Have a different number added and get a different answer.
At first give even numbers to be added. Then, the last time, ask the spectator to add an odd number, such as 9. The final result will now contain a fraction. The spectator, discovering this, is always pleased; he thinks that this will prove too difficult. Let him think that until the last possible moment.
"You are thinking of the figure two . . . but something's wrong! You are also thinking of a one ... and a four. Please don't try to mislead me like that. The answer can't possibly be two hundred and fourteen. Oh, I see .. . you are thinking — four and one-half."
5. the z-ray tube
The performer exhibits a paper cylinder which he says enables him to see through solid objects. He uses it to look through a spectator's hand, through a book, and, finally, demonstrates that it works even for the spectators.
The following three tricks may be done separately, but they are much more effective when presented, as here, in a single routine.
Roll a sheet of paper into a tube about eight inches in length and one inch in diameter. Encircle it with a rubber band.
Place three coins of different denominations on the table or floor and cover them with a book.
Select a spectator to assist you, turn your back, and give him the following instructions: "Lift the book and take out one of the coins. Now decide in which hand you want to hold it, then close your fist tightly on the coin. Place the hand that holds the coin against your forehead and count, aloud, from one to fifteen. Then lower your hand and hold both hands side by side, fists closed."
When this has been done, face the spectator and call attention to the paper tube. "This tube," you say with a straight face, "is a Z-ray machine. It does the same work as an X-ray machine, but it's much better because it is less expensive, it's portable, and you don't have to wait to get the pictures developed. I invented it last night."
Approach the spectator and look through the tube at each of his hands. "You're holding the coin in that hand." Point to the correct hand. (You'll find out how in a moment. )
Go to the book, examine it through the tube for a moment. Turn your back again. "Now, please replace the coin under the book with the others."
After this has been done, turn, take the book away and push each coin forward slightly with your forefinger. "Looking through the book with the Z-ray tube I could see that the quarter (name whichever coin is correct) wasn't there, so that must be the one you were holding."
The Z-ray tube, of course, is entirely misdirection. The secret is much simpler than Z rays. As soon as you turn to face the spectator the first time, glance at his hands. Some of the blood will have left the hand he has been holding to his forehead, and it will be paler than the other.
Another Holmesian clue tells you which coin was used. When you remove the book and push each coin forward, they will all feel slightly cold to the touch except one. This one has picked up heat from the spectator's hand, and is the one you name.
Now for the final astonishing proof that Z rays really work as you claim. Give the tube to a spectator and ask him to look through it. Instruct him to keep both eyes open. Place your hand over the opposite end of the tube.
"Are the Z rays penetrating my hand? Can you see through it?" He says, "No."
"That's odd. All my laboratory tests show that Z rays never fail. Oh. I see. You're looking through the wrong end of the tube. Turn it around."
This time, instead of covering the end of the tube with your hand as before, put it close to the side of the tube, three
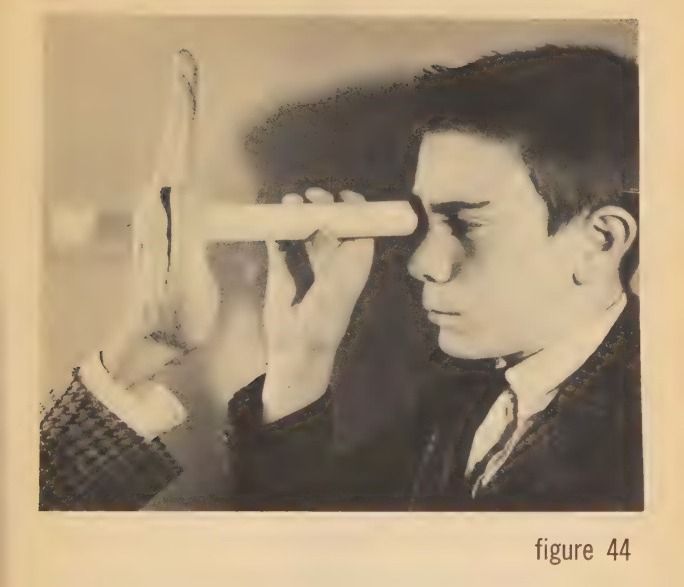
figure 44
or four inches in from the end (fig. 44). The spectator sees a neat round hole drilled right through your hand. The illusion is perfect.
6. Money mind reading
A spectator conceals a nickel in one hand, a dime in the other, and you discover which hand contains which coin.
Tell him to multiply the value of the coin in his right hand by 4, then multiply the value of the coin in the left hand by 7. Ask him to add the two answers and give you the total.
You immediately announce which coin each hand contains. If the answer given is even, the nickel is in the right hand; if odd, the nickel is in the left hand.
This becomes more puzzling if you repeat it, using different multipliers and getting different answers each time. Always ask to have the coin in the right hand multiplied by an even number, the one in the left hand by an odd number.
Now, do it again, but don't ask for the answer. Point to either hand and ask that the value of the coin it holds be multiplied by 16. When the spectator says he has done this, tell him to do the same with the coin in the other hand. As soon as he says he has this answer, tell him which hand holds which coin. Your clue is that it takes him longer to multiply 5 by 16 than 10 by 16.
7. Multiple mind reading
Several spectators mentally select cards, and the performer finds them all. The trick works itself.
From a shuffled deck, deal out five piles of five cards each. Pick up one pile, spread the cards in a fan, show them to a spectator on your left, ask him to mentally select one card and remember it. You must remember that this spectator is No. 1. Square the cards and hold the packet in your left hand.
Show a second group of five cards to a second person whom you remember as being No. 2. Place these five cards in your left hand on the first five. Repeat with three more persons. You must remember which person looked at the first packet, which saw the second, and so on — an easy matter, if you proceed from left to right, in order.
Now deal five cards in a row, then the next five on these, and so on just as you would if you were dealing five hands in a card game.
Pick up any pile, spread the cards in a fan, faces toward the spectators, and ask if anyone sees the card he selected.
Since each group now contains one card from each of the original heaps, the replies you get tell you everything you need to know. If the spectator whom you have remembered as No. 2, because he selected a card from the second heap, says that he now sees his card, you know that it is the second card from the right in the group you hold. If he selected a card from the fourth heap, his card is now fourth from the right.
Sometimes one heap will contain none of the selected cards, and another will contain two or more.
Vary the manner in which you find each card. First, spread the cards out, face up, run your fingers across them, and ask the spectator to think "Stop" when you are pointing at his card. Do the same with the next group, but with the cards face down so that you cannot see the faces. Next time, close your eyes, simply deal the cards, and when you come to the correct one toss it out face up. Finally, hold each card against the spectator's forehead, and pretend to get a vibration on the thought-of card.
These variations are red herrings which conceal the fact that you are counting, and also make your pretense of mind reading more dramatic.
8. X-ray eyes
An extremely mystifying two-person stunt which you and one of your children can do together. You introduce him (or her) as The Boy (or Girl) with X-ray Eyes, and he demonstrates that he can see through various solid objects.
Send him into another room. Then show several coins, one of which is chosen by a spectator and hidden under a cup.
The X-ray Eye wizard returns, looks down through the cup, and not only names the coin but tells which side is up. The test is repeated and made more difficult. The coin is covered by a book, and then by several books, but his phenomenal vision penetrates these just as easily.
An extremely simple signaling system is used, but no one is likely to detect it because it changes each time the feat is repeated. On the first trial, when you cover the coin with the cup, you leave a clue as to the coin's value by the direction in which the cup handle points. If it points north (from your assistant's point of view), the coin is a penny. East indicates a nickel; south means a dime; and west, a quarter.
Any other direction indicates a half dollar.
After the wizard pretends to look through the cup and names the coin, he pauses. Then, if you ask him which side is up, he says "Heads"; but if you say nothing, he says that it is tails up.
He leaves the room again and another coin is selected. You say, "I wonder if he can see through something as thick as this." You cover the coin with a book, and then place the cup on the book. This time leave the cup handle pointing in the same direction as before, but place the book so that its spine faces the direction that indicates the value of the coin.
On the third trial you say, "This time we'll make it really difficult,' and you cover the chosen coin with more books.
This time, it is the number of additional books placed on the coin which gives the clue. One book indicates a penny; two, a nickel; three, a dime; four, a quarter; five, a half dollar.
As a final demonstration which appears far more difficult than anything that has gone before, a playing card, chosen at random and seen by no one, is hidden under the stack of books. The wizard, returning to the room, again uses his X-ray vision and names it.
As you announce this test, you bring out a deck of cards and hold it in such a way that The Boy with the X-ray Eyes can, with a glance in your direction, note the bottom card.
After he leaves the room, shuffle the deck without disturbing the bottom card (page 98), place the deck before a spectator, and ask him to cut it into two portions. Then pick up the lower half of the deck and place it crosswise on the top half.
Now, if you take the attention of the spectators away from the cards for a moment, they will forget exactly what was just done. Turn to the stack of books, lift them off the coin, and remove it.
Then turn back to the cards, lift the upper portion of the deck, slide out the bottom card, and put it to one side, face down. "We'll take the card to which you cut and place it under the books without anyone having seen it."
This is a misstatement because this card is actually the original bottom card of the deck, but if you speak matter-offactly and keep going, no one will doubt you. Pile the books on the card, and perhaps add several more books to make it seem very difficult. :
Recall The X-ray Eye Boy for the grand finale. He should pretend to have great difficulty seeing through so many books. Then he takes one book away, and, still pretending difficulty, names the card. "That's very hard to see because it's face down and I have to look through the card, too. But it seems to be red . . . it is probably a heart .. . and it has five... no, six spots."
Bạn đang đọc truyện trên: AzTruyen.Top