Los sistemas de escritura logo-silábicos de las civilizaciones antiguas empleaban cientos de caracteres distintos; miles en el caso de los más primitivos. Por ello, solo unas pocas personas tenían la posibilidad de alejarse de los fatigosos trabajos manuales y dedicarse durante años a aprender para alcanzar el privilegio de ser escribas. En estas comunidades el conocimiento estaba en posesión de los pocos que sabían leer; el resto, la inmensa mayoría, eran personas iletradas. Por consiguiente, la llegada de los sistemas alfabéticos trajo un soplo de aire fresco, pues para dominarlos y aprender a escribir era suficiente con conocer unas pocas decenas de caracteres. Gracias al alfabeto el conocimiento se popularizaba. Si en las sociedades no alfabéticas éste dependía de solo unos pocos escribas, normalmente vinculados a un palacio o un templo, en el que un rey o unos altos sacerdotes decidían sobre qué se podía escribir; ahora, en las sociedades alfabetizadas había numerosas personas dedicándose a temas y motivaciones de índole diversa.

Sea como fuere, lo cierto es que durante el primer milenio a. C. surge la explosión del saber del mundo griego. En las polis de Asia Menor apareció una figura tan original como sorprendente: el filósofo, un intelectual que amaba el conocimiento en sí mismo y que disfrutaba razonando y argumentando, a menudo sobre temas generales, abstractos y universales. El filósofo era un pensador que solía despreciar el conocimiento útil y práctico para sumergirse en el mundo de las ideas teóricas 41. Lo importante es que esas matemáticas de los escribas —egipcios y mesopotámicos— del pasado, orientada a solucionar problemas útiles y que a menudo quedaban resueltos de forma cortoplacista, tosca e improvisada, dejó paso al análisis de esos mismos temas y otros nuevos a la manera profunda, sosegada y teórica del filósofo, quien las enmarcaba en un contexto más amplio y permitía identificar cuestiones subyacentes, sutilezas a menudo no percibidas por sus antecesores.

El espíritu griego se apoyó en los conocimientos de los escribas mesopotámicos y egipcios y, desde esa base, aportó su original forma de hacer matemáticas. Entre todas sus contribuciones quizá la más importante fue el método deductivo, la necesidad de que cada resultado fuera probado utilizando el poder de la lógica. La demostración matemática apareció desde el principio del amanecer griego y fue la piedra de toque sobre la que se fundamentó toda la construcción de sus matemáticas. La necesidad de coherencia implicó la aparición de conclusiones inesperadas que les permitieron intuir la fisonomía de las matemáticas del futuro. El matemático más antiguo conocido del que se dice que realizó una demostración es del siglo VI a. C., fue Tales de Mileto 42.

Aunque había matices y discrepancias entre las distintas escuelas filosóficas, el concepto de número en Grecia, a diferencia de las civilizaciones que habían precedido, se definió de forma precisa. Los griegos interpretaban el número, la cantidad, como una «pluralidad de individuos»; es decir, el resultado de un proceso de conteo, bien sea de elementos indivisibles o de magnitudes continuas medidas con una unidad de medida. Damos la explicación de Aristóteles:

Se dice que posee «cantidad» lo que es divisible en partes internas, cada una de las cuales —sean dos o más de dos— sean por naturaleza uno, y algo determinado. Una pluralidad es una cantidad si es numerable, y también lo es una magnitud si es mensurable. Se llama «pluralidad» lo potencialmente divisible en partes discontinuas y «magnitud» lo divisible en partes continuas. 43

No obstante, el uno no solía ser considerado número pues no encajaba en el concepto de «pluralidad de individuos». El cero, como sabemos, ni siquiera era conocido por los griegos.

«Uno» significa que es medida de cierta pluralidad, y «número» que se trata de una pluralidad medida y de una pluralidad de medidas (por eso, lógicamente, el uno no es un número, ya que tampoco la medida es medidas, sino que la medida y el uno son el principio). 44

Estamos hablando del número como número natural, pues la fracción —empleada en medir magnitudes continuas—, no era un número en sí mismo, sino un par de números, los dos que la componen:

Por otra parte, no siempre la medida es una, sino que a veces es más de una: así, las diesis son dos —que no se perciben con el oído, pero se dan en las proporciones numéricas—, y más de una son las voces con las que medimos, y con dos se miden la diagonal y el lado, y las magnitudes todas. 45

Entre los primeros matemáticos griegos de cierta importancia destacó Pitágoras, una figura cuya imagen ha sido tan distorsionada y deformada que pocas cosas pueden asegurarse con certeza sobre él. Como referencia, aportemos algunos detalles básicos. Nació en Samos, en la costa jónica (Grecia asiática) durante el comienzo del siglo VI a. C.. Tras un periodo de formación quizá en Oriente o en Egipto, al volver a Samos se vio forzado a abandonar el lugar donde había nacido. Decidió establecerse en la Magna Grecia, en el sur de Italia, fundando allí la llamada escuela pitagórica, una congregación mística, religiosa, política y también científica, que aportaría matemáticos sobresalientes.

Se atribuye a Pitágoras el descubrimiento y la demostración del famoso teorema que lleva su nombre, y que nos asegura que, en un triángulo rectángulo cualquiera, la suma del cuadrado de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa. Como en todo lo relacionado con Pitágoras, sobre este tema han surgido numerosas dudas. Parece razonable considerar que la demostración de este teorema, tan ampliamente utilizado por otros matemáticos, es de Pitágoras o de sus más directos discípulos, ya que en épocas anteriores no se realizaban demostraciones matemáticas. Sin embargo, el teorema en sí o incluso la utilización de las llamadas ternas pitagóricas, es decir, grupos de tres números naturales que verifican el teorema pudo ser conocido por civilizaciones anteriores.

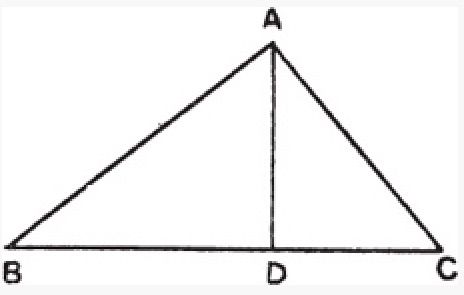
No se sabe qué demostración realizaron los primeros pitagóricos de este teorema. Detallamos una sencilla basada en la semejanza entre triángulos —distinta a la más geométrica que aparece en Elementos y que podría ser posterior o no, realmente no se sabe con certeza—. La idea es que el triángulo rectángulo ABC es semejante al ADC (con D el punto en el que la hipotenusa corta a la perpendicular que pasa por el vértice). Entonces, por semejanza entre triángulos, se deduce: BC / AC = AC / DC. Despejando:

AC2  = BC DC

Trabajando análogamente con el otro cateto se llega a una expresión simétrica:

AB2  = BC DB

Sumando ambas expresiones obtenemos

AC2  + AB2 = BC DC+ BC DB = BC (DC + DB) = BC2

El razonamiento es correcto en nuestro sistema numérico; pero, como curiosidad, hay que señalar que podría ser criticado dentro del rígido esquema pitagórico, ya que las operaciones aritméticas que se aplican sobre BC / AC parten de la presunción de que esta expresión es una fracción entre dos números naturales, algo que no se ha probado en el desarrollo de la demostración de este teorema. Es posible que alguna situación similar a ésta empujase a los pitagóricos a analizar la relación entre cateto y la hipotenusa del triángulo o, expresado de otra manera, entre el lado y la diagonal del rectángulo.

Otro importante componente de la escuela pitagórica se llamaba Filolao de Crotona. Vivió durante el siglo V a. C. en la zona de la Magna Grecia. Lo interesante es que, a diferencia del fundador de la escuela pitagórica, Filolao sí dejó por escrito algunos textos, abarcando desde su concepción del pitagorismo, hasta sus ideas de Astronomía y Cosmología, pasando por sus planteamientos sobre el concepto de número. Aunque por desgracia sus obras no han sobrevivido íntegras al paso de los siglos, algunos aspectos de su pensamiento pueden reconstruirse gracias a los escasos fragmentos de estos textos que sí se han conservado. Son muy importantes, porque el mensaje original de Pitágoras ha sido muy distorsionado por el paso de los siglos, sin embargo, estos pequeños textos fueron escritos por uno de sus sucesores más directos.

Así, es conocido que Aristóteles explicaba que los pitagóricos defendían que «todo es número»:

Pues bien, también ellos [los pitagóricos] parece que piensan que el número es principio que constituye no sólo la materia de las cosas que son, sino también sus propiedades y disposiciones, [...]

Es decir, según Aristóteles, los pitagóricos consideraban que las cosas estaban físicamente «hechas de números», siendo el número el fundamento ¿material? del universo. Pero, si leemos a Filolao —anterior a Aristóteles— esto no es exactamente así. Tal como él mismo explicaba (fragmento 4):

En efecto, todas las cosas que se conocen tienen número, porque sin él no podemos entender ni saber nada.

En este texto el planteamiento no es ontológico, sino epistemológico: las cosas no están «hechas de números» sino que «tienen números». El número permite conocer el universo, es decir, las cosas pueden ser contadas y medidas. Las cosas tenían números, ya sea porque fueran contables con números naturales o medibles empleando fracciones entre números naturales, como es el caso de las medidas continuas de la Geometría. En conclusión, según Filolao, los pitagóricos consideraban que las cosas conocidas son conocidas gracias al número, un planteamiento enormemente moderno para la época y mucho más plausible que el que sugiere Aristóteles.

La Aritmética pitagórica estudiaba diversas propiedades de los números, clasificándolos de múltiples maneras: números pares e impares, números primos y compuestos, números amigos, números perfectos, números lineales, planos, sólidos, oblongos, cúbicos, triangulares, cuadrados, pentagonales, hexagonales... De esta manera, se dedicaron a estudiar con entusiasmo las propiedades más sencillas de los números naturales. Por ejemplo, descubrieron que los números cuadrados

●  ●      ●  ●  ●      ●  ●  ●  ●
●  ●      ●  ●  ●      ●  ●  ●  ●
            ●  ●  ●      ●  ●  ●  ●
                            ●  ●  ●  ●

cada uno podía obtenerse del anterior añadiendo un número impar. En nuestra terminología sería:

(n + 1)2 - n2 = 1 + 2n

Ya vimos en el capítulo anterior la fusión entre Astronomía y astrología que era habitual en los estudiosos de Mesopotamia. El caso de los pitagóricos no parecía muy distinto, pues el misticismo se entrelazaba con los resultados matemáticos. Por ejemplo, el número 10 (un número triangular, suma de 1, 2, 3 y 4), la llamada tetraktys, tenía para ellos un significado esotérico, y era representado con unos puntos dispuestos formando un triángulo.

●
●  ●
●  ●  ●
●  ●  ●  ●

La aritmética de los pitagóricos antiguos era una teoría de números de «guijarros en el suelo», con un planteamiento discreto, no contínuo. Debió ser habitual que los pitagóricos acumulasen pequeños guijarros en montoncitos para realizar sus cálculos o dispusieran las piedrecitas para formar figuras geométricas.

Existían para ellos cuatro grandes campos del saber: la Aritmética, como ya hemos visto, pero también la Geometría, la Música y la Astronomía. La más importante era la primera, pues todas las demás eran conocidas por objetos que tenían números o fracciones de números, tal como explicaba Filolao.

No solo las magnitudes de la Geometría podían ser medidas y tenían un número, la Música, por su parte, también los tenía. Las armonías musicales se disponían siguiendo las relaciones de las proporciones entre números sencillos. Así, en los instrumentos de cuerda, las cuerdas sometidas a la misma tensión basaban sus armonías en las relaciones de sus longitudes: la octava es ½, la quinta es ⅔ y la cuarta, ¾. Asimismo, la Astronomía tenía números, en la que los cuerpos celestes se ordenaban en el Cosmos siguiendo armonías similares a las de la Música. Se hablaba de una Armonía de las Esferas en la que los astros53, en su movimiento perpetuo, producían ciertas melodías. Estos descubrimientos son atribuidos por la tradición a Pitágoras, y a menudo van acompañados de leyendas más o menos inverosímiles.

Es importante señalar que sus «instrumentos matemáticos de medida», es decir, los conceptos numéricos con los que describían el resultado de sus medidas seguían consistiendo en los números naturales para las cantidades discretas y las fracciones para magnitudes continuas. Inicialmente, el recipiente numérico empleado para recoger los resultados de sus medidas era, por tanto, ℚ+, el mismo que habían empleado egipcios y babilonios. Y fue así al principio, hasta que irrumpió en la escena uno de los sucesores de Pitágoras: Hipaso de Metaponto. Este pitagórico vivió en la Magna Grecia a caballo entre los siglos VI y V a. C.. Fue un notable matemático (se le atribuye la construcción del dodecaedro), y es él a quien la tradición asigna el descubrimiento de un hecho tan inesperado como sorprendente, que haría saltar por los aires todos estos esquemas de pensamiento. Se supone que fue Hipaso quien analizando la longitud de la diagonal del cuadrado demostró que esta magnitud era «inconmensurable» con su lado, es decir: no era medible. Las magnitudes geométricas rara vez podían describirse con números naturales, más bien solían ser el resultado de comparar una unidad de medida con la magnitud a medir, y se expresaban como una expresión racional, una fracción. Pues bien, los primeros pitagóricos demostraron matemáticamente que la diagonal del cuadrado unitario no podía ser una fracción. Es decir, en la aritmética pitagórica no existía ningún número o fracción de números que permitiera medir la diagonal del cuadrado. No había número, ni había medida, por consiguiente: la diagonal del cuadrado, era inconmensurable con el lado del cuadrado. Más adelante definiremos qué significa «inconcmensurable», este concepto tan esencial.

Pero, ¿a qué tanto revuelo con este número? Después de todo, √2 —la medida de la diagonal del cuadrado unitario— era un viejo conocido de los matemáticos babilonios. La tablilla cuneiforme YBC 7289 del milenio II a. C. muestra una tosca diagonal en un cuadrado acompañada del valor de √2 con una precisión equivalente a seis posiciones decimales correctas... Todo un mérito para la rudimentaria matemática de los escribas de Mesopotamia. La diferencia estribaba en que la capacidad teórica de los griegos y su andamiaje axiomático y deductivo actuaban como un potente microscopio matemático que ponía de relieve detalles sutiles que habían pasado desapercibidos para otras civilizaciones: ellos comprendieron que √2, este viejo conocido, no era una fracción entre dos números naturales.

La demostración de la irracionalidad de √2 es sencilla y disponemos de la que probablemente realizaron los primeros pitagóricos. Sea AB el lado del cuadrado y AC su diagonal. Procedemos por reducción al absurdo partiendo de la afirmación de la hipótesis, es decir:

AC / AB = α / β con α y β dos números (naturales) primos entre sí, expresados por tanto con los números más pequeños que es posible encontrar. Ahora bien, aplicando el teorema de Pitágoras sobre el cuadrado se cumple que AC2 = AB2 + AB2 = 2 AB2 , por tanto:

α2 / β2 = AC2 / AB2 = 2

α2 = 2 β2

Es decir, α2 es par y, por consiguiente, α es par. Pero, como α y β son primos entre sí, β debe ser impar. Pero α es par y puede ser expresado α = 2 γ, para algún número γ. Por consiguiente:

2 β2 = α2 = (2 γ)2 = 4 γ2

Es decir, β2 = 2 γ2 , pero habíamos dicho que β debe ser impar, lo cual es una contradicción.

La conclusión es que AC es inconmensurable con AB54.

Los pitagóricos aseguraban que «todas las cosas que se conocen tienen número»; pero esto no parecía cumplirse para la diagonal del cuadrado. La crisis de los inconmensurables cuando menos supuso un inconveniente importante para esta escuela pitagórica, pues ponía de manifiesto que existían conceptos geométricos importantes más allá de la teoría de la medida aportada por el pitagorismo55.

Y, a partir de ahí, las cosas empeoraron. Por si la inquietante aparición de √2 no fuera suficiente, Teodoro de Cirene56 fue capaz de demostrar que junto a √2, también √3, √5, √6, √7... hasta √17 tampoco eran números o fracciones57. √2 no era un caso aislado, estos «inconmensurables» abundaban, de hecho, aparecían por doquier.

Posteriormente, el discípulo más capaz de Teodoro, Teeteto de Atenas, gran amigo de Platón y uno de los más brillantes matemáticos del periodo (se le atribuye la construcción del icosaedro y el octaedro) hizo avanzar todavía más la ciencia de los irracionales, demostrando que para cualquier número (natural) no cuadrado n, la expresión √n no era racional58... La Geometría parecía infestada de estas inquietantes magnitudes patológicas que se negaban a comportarse siguiendo los dogmas pitagóricos.

Y había más casos59. Si la diagonal del cuadrado era irracional, también lo era la diagonal del pentágono (diagonal entendida como el segmento que une dos vértices no consecutivos). La diagonal del pentágono era inconmensurable con su lado, y toma el valor φ = (1+√5)/2 (=1,6180...), la llamada sección áurea. La primera definición60 conocida de este importantísimo número aparece en los Elementos de Euclides, con la demostración de su irracionalidad61, pero se sospecha que fue estudiada mucho antes por los primeros pitagóricos, quienes concedían una enorme relevancia esotérica al pentagrama místico, la estrella de cinco puntas formada con las cinco diagonales de un pentágono.

La diagonal del cuadrado y otras muchas magnitudes geométricas no encontraban número ni fracción dentro de la rígida aritmética pitagórica. Poco a poco, la Geometría, una ciencia segura en la que los resultados podían quedar «geométricamente demostrados» con regla y compás (sin emplear números) fue tomando la iniciativa y desplazando a la insegura Aritmética. Incluso en los escasos fragmentos que nos han llegado de los textos de Arquitas de Tarento, uno de los últimos pitagóricos, se observa una especie de «geometrización» de la teoría de los números, representados ahora como segmentos de recta62. Tras el final de la escuela pitagórica63, a mediados del siglo IV a. C., el pensamiento ateniense dominaba el panorama; y gracias a la beneficiosa influencia de Platón, numerosos filósofos se interesaban por las Matemáticas64 —como fue el caso de Teeteto— haciendo especial énfasis en la Geometría, a la que aportarían numerosos resultados.

Un tiempo después, cuando cerca del año 300 a. C. el platónico Euclides de Alejandría compilaba el saber matemático de su tiempo en los trece libros que componen su famosa obra Elementos, la teoría de los números se mostraba como una rama dependiente y subordinada a la Geometría. Euclides presentaba los resultados de forma «geometrizada» 65 «especialmente en el álgebra del libro II) expresando las cantidades como segmentos de recta; la aritmética que se leía en la obra de Euclides (libros VII, VIII y IX) recogía los resultados siglos atrás descubiertos por los pitagóricos; pero estaba ya muy lejos de esa primera aritmética pitagórica «de guijarros en el suelo».

El paso al frente de la Geometría de regla y compás, sin números, supuso una transformación en el esquema general, un cambio que parece relacionado con la crisis de los inconmensurables en la Geometría, esas magnitudes matemáticas no entendibles dentro de la rígida aritmética pitagórica, que ahora quedaba arrinconada y bajo sospecha. Sin embargo, poner la Geometría en primer plano suponía ceder el protagonismo a esas misteriosas magnitudes inconmensurables, y eso constituía nada menos que el comienzo de la entronización del número real, como veremos más adelante.

Hay acuerdo entre los expertos66 en que el libro X de los Elementos de Euclides contiene los principales resultados obtenidos por Teeteto de Atenas, el gran estudioso griego de los irracionales. Es posible, no obstante, que algunos detalles técnicos adicionales fueran incorporados por matemáticos posteriores67, entre ellos el propio Euclides, en su afán por sistematizar y poner coherencia en todos sus elementos.

Sea como fuere, lo importante es que el libro X es el primer tratado sobre números irracionales que se conserva68 en el que su autor es consciente de que está trabajando con algo que no son fracciones. Nada menos. La humanidad comenzaba la aventura del estudio de los primeros irracionales, y lo hacía con la misma torpeza con la que el hombre del neolítico había abordado los números naturales. Ya hemos visto las barreras intelectuales que tuvieron que superarse hasta disponer de un sistema numérico eficiente; con los irracionales pasó algo similar, y no será hasta la Edad Moderna cuando una notación algebraica eficiente facilitase los tratamientos. En aquellos tiempos de los griegos los inconmensurables no eran considerados números. Por ello, este tratado de irracionales está geometrizado, no aparecen en él expresiones algebraicas ni fórmulas de ningún tipo. El intrincado libro X, la llamada «cruz de los matemáticos», es difícil de leer y no solo por la notación farragosa y por su extensión —con mucho el más largo de Elementos—, sino por la dificultad de encontrar coherencia en los resultados y adivinar los propósitos del autor de tan complicado texto. Si en la Aritmética los griegos mostraban rigideces (como considerar que el uno no era un número o solo aceptar las fracciones como pares de números), en lo tocante a los irracionales también afloraban numerosos prejuicios. El libro X trata los irracionales, especialmente los que —desde la visión imperante— pueden construirse con regla y compás. En su mayoría son elaboraciones geométricas reflejo de expresiones aritméticas con raíces cuadradas y alguna raíz cuarta.

Daremos algunos detalles sobre el texto. Se comienza con la definición de conmensurable. Dos magnitudes son conmensurables si «se miden con la misma medida», es decir, si existe una medida en común «que las mida» conjuntamente. Tomemos algunos ejemplos:

Dos segmentos de longitudes 3 y 6. 3 es múltiplo de 6 quiere decir que «3 mide a 6». Son conmensurables.
Dos segmentos de longitudes 3 y 5. 3 no es múltiplo de 5. «3 no mide a 5», pero en este caso se puede tomar una medida en común (la unidad) que sí los mide. Son conmensurables.
Dos segmentos de longitudes 3 y √3. En este caso no se puede encontrar una medida en común que los mida. Son inconmensurables.

El libro X incluye un criterio para determinar si dos magnitudes son inconmensurables. Este nuevo método (Antifairesis 69) es general y distinto al utilizado en la demostración que hemos visto de la irracionalidad de la diagonal del cuadrado unitario, prueba realizada siglos atrás por los primeros pitagóricos. En la  Antifairesis, dadas dos magnitudes, el algoritmo irá siempre restando la menor de la mayor, buscando en cada iteración la unidad común que las mida. Tomemos algún ejemplo:

Dos segmentos de longitudes 3 y 5 (no se miden, pues la menor no es múltiplo de la mayor). Restamos el menor al mayor, de 3 a 5, y el resultado sustituye al mayor, a 5, dando 3 y 2. Siguen sin medir. Restamos 2 a 3 y quedan 2 y 1. 1 mide a 2. Son conmensurables. Es decir, en nuestra notación moderna diríamos que la fracción ⅗ es racional.

Teeteto procede pues a la clasificación de los irracionales más sencillos. De este modo, se analizan expresiones que son operaciones simples de magnitudes sólo conmensurables en cuadrado (como √2 o √3, que son inconmensurables, pero cuyo cuadrado es conmensurable). Se estudia la suma (llamada binomial70, asociada por Papo a la media aritmética) y la resta (apótoma 71, que se suponía relacionada con la media armónica) . Por último, la medial72 se define como el lado de un cuadrado con la misma área que un rectángulo irracional, es decir, algo similar a la media geométrica de dos magnitudes sólo conmensurables en cuadrado. Estas tres definiciones serán la base para la clasificación de trece categorías distintas de irracionales73.

En palabras de Papo de Alejandría 74:

Fue Teeteto quien distinguió las potencias (cuadrados) que son conmensurables de aquellas que son inconmensurables (en longitud), y quien dividió las líneas irracionales más generalmente conocidas según los diferentes medios, asignando la medial a la geometría, el binomio a la aritmética y la apótoma a la armonía [...].

Números algebraicos

Por primera vez en la historia se superaba la frontera de los números racionales positivos ℚ+ para adentrarse conscientemente en el conocimiento de los primeros irracionales. Dada la dificultad de la empresa en la que se aventuraban, comenzaban el estudio con suma prudencia, incluyendo en Elementos los casos más sencillos para ellos: los irracionales construibles con regla y compás. Los griegos se adentraban en el estudio de  los irracionales y, titubeantes, lo hacían comenzando por expresiones sencillas de raíces cuadradas y raíces cuartas. Estos casos irracionales pertenecen al conjunto 𝔸ℝ+, el conjunto de los números algebraicos reales positivos, es decir, que pueden obtenerse como raíces de polinomios con coeficientes enteros. Por ejemplo, √2 es la solución de la expresión algebraica x2 - 2 = 0:

ℕ ⊂ ℤ ⊂ ℚ ⊂ 𝔸ℝ

Aunque 𝔸ℝ es un conjunto más amplio que ℚ, su cardinal infinito sigue siendo «el infinito más pequeño», es decir, ℵ0.

ℵ0 = |ℕ| = |ℤ| = |ℚ| = |𝔸ℝ|

A excepción de los elementos de ℚ, la expresión decimal de los de 𝔸ℝ será infinita y no periódica. Así, los racionales ¼ = 0,25 y ⅓ = 0,33333... = 0,3̑, pero √2 = 1,414213562373...

Pero la aventura había comenzado y era imparable. Aunque no aparecerían en Elementos, ya en aquella época se estaban descubriendo nuevos especímenes en el bestiario matemático, magnitudes aún más extremas que las aquí descritas y de muy difícil encaje en estos rígidos esquemas teóricos.

Aristóteles. Metafísica. Gredos. 2007.
Aristóteles. Tratados de lógica. Analíticos Primeros. Gredos. 2007.
Corry, Leo. The Development of the Idea of Proof. Dentro de Princeton Companion to Mathematics, editado por Timothy Gowers. 2008.
Diógenes Laercio. Vidas. Gredos. 2009.
Euclides. Elementos. Vol. I y II. Gredos. 2007.
Euclides.The Thirteen Books of the Elements. Vol. 1, 2 y 3. Comentado y traducido por Sir Thomas L. Heath. Cambridge University Press. 1968.
Fowler, D. H.. An Invitation to Read Book X of Euclid's Elements. Historia Mathematica, 19. 1992.
Gambra, José Miguel. El número en Aristóteles. La ciencia de los filósofos. 1996.
Huffman, Carl. The role of number in Philolaus' Philosophy. 1987.
Knorr, Wilbur Richard. The Evolution of the Euclidan Elements. D. Reidel Publishing Company. 1975.
Taylor, Thomas. The Commentaries of Proclus on the First Book of Euclid's Elements of Geometry. 1792.
Thomson, William; Junge, Gustav. The Commentary of Pappus on Book X of Euclid's Elements. Harvard Semitic Studies, vol. 8. 1930.
Morrow, G. N.. Proclus: A Commentary on the First Book of Euclid's Elements. Princeton University Press, 1970.
Platón. Diálogos V. Teeteto. Gredos. 2007.
Zhmud, Leonid. Early Mathematics and Astronomy. Oxford Handbook of Science and Medicine in the Classical World. Oxford University Press. 2018.
Zhmud, Leonid. Pythagoras and the early pythagorenas . Cambridge University Press. 2012.
Zhmud, Leonid. From Number Symbolism to Arithmology. Zahlen-und Buchstabensysteme im Dienste religiöser Bildung. 2019.
Zhmud, Leonid. Pythagorean Number Doctrine in the Academy. On Pythagoreanism 5. 2013.

41. De cualquier forma, esta descripción genérica no debería hacernos olvidar que algunos de ellos combinaron la teoría y el conocimiento aplicado, llegando a ser ingenieros muy notables.
42. Ver The Development of the Idea of Proof de Leo Corry. Diógenes Laercio en sus Vidas cuenta de Tales de Mileto que fue capaz de medir la altura de las pirámides egipcias analizando la longitud de la sombra que estas proyectaban sobre el suelo.
43. Aristóteles. Metafísica. Libro V. Gredos. 2007.
44. Elementos. Euclides. VII. D1 y D2:
1. Una unidad es aquello en virtud de lo cual cada una de las cosas que hay es llamada una.
2. Un número es una pluralidad compuesta de unidades.
45. Aristóteles. Metafísica. XIV. Gredos. 2007.
46. Aristóteles. Metafísica. X. Gredos. 2007.
47. El caso más sencillo es 3, 4 y 5, ya que 32 + 42 = 52. Otro ejemplo, es 62 + 82 = 102; también 52 + 122 = 132. Se pueden construir fácilmente partiendo de dos números naturales p y q para calcular los catetos p2 - q2, 2pq y la hipotenusa p2 + q2.
48. Elementos. Euclides. I. P47.
49. The role of number in Philolaus' Philosophy, de Carl Huffman. 1987.
50. Aristóteles. Metafísica. I. Gredos. 2007.
51. Tomado de Early Mathematics and Astronomy de Leonid Zhmud en Oxford Handbook of Science and Medicine in the Classical World. 2018.
52. «[...] los primeros pitagóricos representaban los números [...] mediante psephoi, contando piedras». Early Mathematics and Astronomy. Leonid Zhmud.
53. Un concepto que influiría mucho en el físico y matemático Johannes Kepler.
54. «[...] como, por ejemplo, que la diagonal es inconmensurable [se prueba] porque lo impar se hace igual a lo par al suponer que sea conmensurable. Así pues, que lo par se hace igual a lo impar se prueba por razonamiento; en cambio, que la diagonal es inconmensurable se demuestra por hipótesis, ya que en virtud de la contradicción se desprende una falsedad». Analíticos Primeros. I. 23. Aristóteles. Gredos. 2007.
55. Sobre este asunto hay debate entre los entendidos para determinar la importancia que esta situación tuvo en las matemáticas griegas. Las interpretaciones van desde una paralizante crisis en los fundamentos (Heath) hasta una visión mucho más aligerada (Knorr). Por nuestra parte, no teniendo otra pretensión que mostrar una historia de algunos conceptos matemáticos contemplados desde el punto de vista de la medida matemática, aunque no hablamos de una crisis devastadora, tampoco podemos minimizar el hecho de que algunas magnitudes geométricas no tuvieran medida en el panorama intelectual griego.
56. Llegó a ser uno de los matemáticos más importantes del siglo V a. C., posible pitagórico, fue profesor de matemáticas del mismísimo Platón.
57. TEETETO: «Con respecto a las potencias, Teodoro nos hizo un dibujo para demostrarnos que las de tres pies no son conmensurables en longitud con las de uno, y las fue eligiendo así, una a una, hasta la de diecisiete pies. Pero se detuvo en este por alguna razón. Así que se nos ocurrió que podríamos intentar reunir todas las potencias, ya que parecían ilimitadas en número, bajo la denominación de un mismo término». Teeteto. Platón. Gredos. 2007.
58. Elementos. Euclides. X. P9.
59. Uno de los casos que no trataremos aquí son las razones superparticulares (expresiones del tipo (N+1)/N, con N natural), cuya raíz cuadrada es irracional según mostró Arquitas de Tarento en sus estudios sobre teoría de la música. Ver Knorr, The Evolution of the Euclidean Elements.
60. Elementos. Euclides. VI. D3.
61. Elementos. Euclides. XIII. P6 y P8.
62. «[...] los primeros pitagóricos representaban los números no mediante segmentos de recta, como lo hicieron Arquitas (DK 47 A 19) y Euclides [...]». Early Mathematics and Astronomy. Leonid Zhmud.
63. El ideal pitagórico resurgiría (es posible que algo distorsionado por el paso de los siglos) revitalizado dentro del movimiento neopitagórico (siglos I a III d. C.), dando lugar a que se escribieran obras aritméticas fuertemente impregnadas del estilo pitagórico y que han sido conservadas hasta la actualidad. Me refiero a Nicómaco de Gerasa (año 100 d. C., aproximadamente) con su Introducción a la Aritmética, que produjo una notable influencia en la sociedad moderna.
64. Como atestigua Proclo en sus comentarios a los Elementos de Euclides.
65. Knorr sugiere que esta «geometrización» pudo ser impulsada por Teodoro de Cirene. Ver The Evolution of the Euclidean Elements.
66. Leer los comentarios de Papo de Alejandría al libro X de Elementos de Euclides.
67. Según Proclo, entre ellos estaba Hermotimus de Colofón, de quien solo conocemos el nombre.
68. Tuvo que haber algunos tratados anteriores sobre el tema que se han perdido. Al margen de que Teodoro y Teeteto pudieron dejar escrito algún texto, Diógenes Laercio en su obra Vidas nos habla de algún tratado de irracionales escrito por Demócrito de Abdera, el atomista, quien llegó a ser un notable matemático. A esto hay que añadir que la de Euclides era la cuarta versión de Elementos que se escribía; la primera es del siglo V a. C y se atribuye a Hipócrates de Quíos, de quien hablaremos en el siguiente capítulo.
69. Elementos. Euclides. X. P2.
70. Elementos. Euclides. X. P36.
71. Elementos. Euclides. X. P72.
72. Elementos. Euclides. X. P21.
73. Según Papo de Alejandría, posteriormente a Euclides el célebre matemático Apolonio de Perga (siglo III a. C.) escribiría una obra (hoy perdida) sobre irracionales, más profunda que la de Teeteto, ampliando las binomiales a trinomiales y más allá, en la que también estudiaba nuevas categorías más generales, que denominó «irracionales desordenados»
74. The Commentary of Pappus on Book X of Euclid's Elements.