1. Hợp và giao của các tập hợp

+ Hợp của hai tập hợp A và B (kí hiệu 𝐴∪𝐵) là tập hợp gồm các phần tử thuộc tập hợp A hoặc thuộc T.

𝐴∪𝐵={𝑥|𝑥∈𝐴 hoặc 𝑥∈𝐵}.

+ Giao của hai tập hợp A và B (kí hiệu 𝐴∩𝐵) là tập hợp gồm các phần tử thuộc cả hai tập hợp A và B.

𝐴∩𝐵={𝑥|𝑥∈𝐴 và 𝑥∈𝐵}.

+ Nhận xét: Nếu A và B là hai tập hợp hữu hạn thì

𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵)
Nếu 𝐴∩𝐵=∅ thì 𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)

2. Hiệu của hai tập hợp, phần bù của tập con

Hiệu của hai tập hợp A và B (kí hiệu 𝐴∖𝐵) là tập hợp gồm các phần tử thuộc A nhưng không thuộc B.

𝐴∖𝐵={𝑥|𝑥∈𝐴 và 𝑥∉𝐵}.

Nếu 𝐴⊂𝐸 thì 𝐸∖𝐴được gọi là phần bù của A trong E, kí hiệu là 𝐶𝐸𝐴.

Ví dụ: 𝐶ℤℕ=ℤ∖ℕ={𝑥|𝑥∈ℤ và 𝑥∉ℕ}={...;−3;−2;−1}
Đặc biệt: 𝐶𝑆𝑆=∅

Bài tập

Có 2 đường tròn chia một hình chữ nhật thành các miền như hình bên. Hãy đặt mooix thẻ số sau đây vào miền thích hợp trên hình chữ nhật và giải thích cách làm

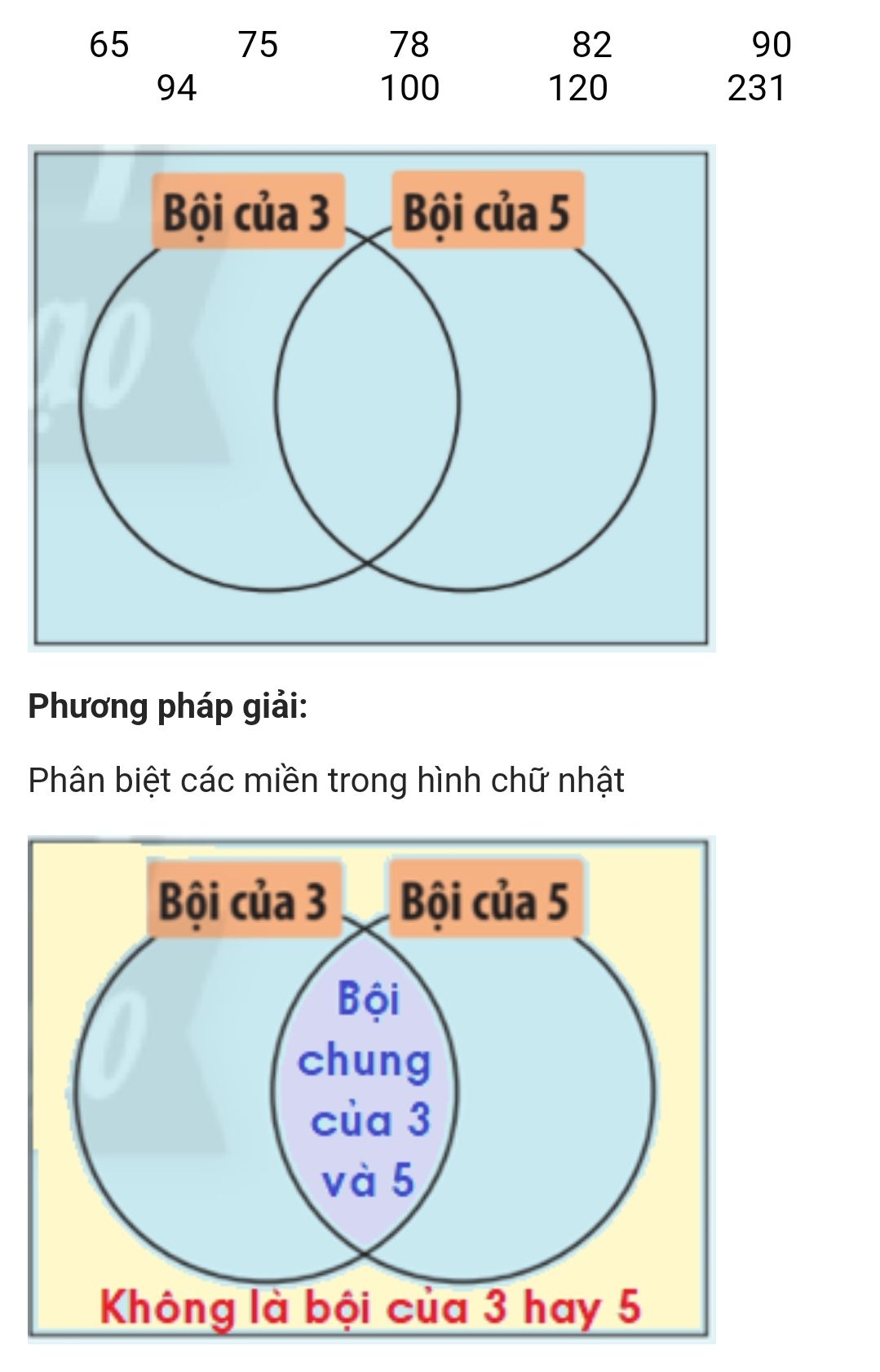
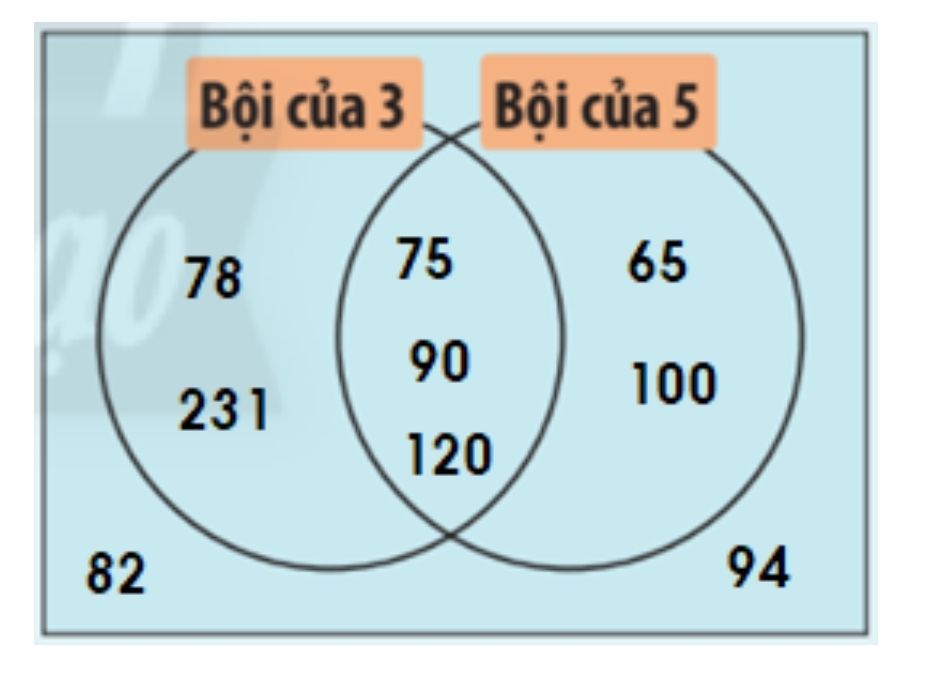
Lời giải chi tiết:

Bội của 3: 75, 78, 90, 120, 231

Bội của 5: 65, 75, 90, 100, 120

Vừa là bội của 3, vừa là bội của 5: 75, 90, 120.

Không là bội của 3 và không là bội của 5: 82, 94

a) Xác định tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn, tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ.

b) Xác định tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ.

c) Xác định tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ.

a) Tập hợp A gồm các ứng viên đạt yêu cầu về chuyên môn là:

𝐴={𝑎1;𝑎2;𝑎5;𝑎6;𝑎7;𝑎8;𝑎10}

Tập hợp B gồm các ứng viên đạt yêu cầu về ngoại ngữ là:

𝐵={𝑎1;𝑎3;𝑎5;𝑎6;𝑎8;𝑎10}

b) Tập hợp C gồm các ứng viên đạt yêu cầu cả về chuyên môn và ngoại ngữ là:

𝐶={𝑎1;𝑎5;𝑎6;𝑎8;𝑎10}

c) Tập hợp D gồm các ứng viên đạt ít nhất một trong hai yêu cầu về chuyên môn và ngoại ngữ là:

𝐷={𝑎1;𝑎2;𝑎3;𝑎5;𝑎6;𝑎7;𝑎8;𝑎10}

Xác định các tập hợp 𝐴∪𝐵 và 𝐴∩𝐵, biết:

a) 𝐴={𝑎;𝑏;𝑐;𝑑;𝑒}, 𝐵={𝑎;𝑒;𝑖;𝑢}

b) 𝐴={𝑥∈ℝ|𝑥2+2𝑥−3=0},𝐵={𝑥∈ℝ||𝑥|=1}

Phương pháp giải:

𝐴∪𝐵={𝑥|𝑥∈𝐴 hoặc 𝑥∈𝐵}

𝐴∩𝐵={𝑥|𝑥∈𝐴 và 𝑥∈𝐵}

a) 𝐴∪𝐵={𝑎;𝑏;𝑐;𝑑;𝑒;𝑖;𝑢}, 𝐴∩𝐵={𝑎;𝑒}

b) Phương trình 𝑥2+2𝑥−3=0 có hai nghiệm là 1 và -3, nên 𝐴={1;−3}

Phương trình 𝐵={𝑥∈ℝ||𝑥|=1} có hai nghiệm là 1 và -1, nên 𝐵={1;−1}

Từ đó, 𝐴∪𝐵={1;−1;−3}, 𝐴∩𝐵={1}.

Cho 𝐴={(𝑥;𝑦)|𝑥,𝑦∈ℝ,3𝑥−𝑦=9}, 𝐵={(𝑥;𝑦)|𝑥,𝑦∈ℝ,𝑥−𝑦=1}
Hãy xác định 𝐴∩𝐵.

Phương pháp giải:

𝐴∩𝐵={(𝑥;𝑦)|(𝑥;𝑦)∈𝐴 và (𝑥;𝑦)∈𝐵}
Lời giải chi tiết:

a) 𝐴∩𝐵={(𝑥;𝑦)|𝑥,𝑦∈ℝ,3𝑥−𝑦=9,𝑥−𝑦=1}

Tại vòng chung kết của một trò chơi trên truyền hình, có 100 khán giả tại trường quay có quyền bình chọn cho hai thí sinh A và B. Biết rằng có 85 khán giả bình chọn cho thí sinh A, 72 khán giả bình chọn cho thí sinh B và 60 khán giả bình chọn cho cả hai thí sinh. Có bao nhiêu khán giả đã tham gia bình chọn? Có bao nhiêu khán giả không tham gia bình chọn?

Phương pháp giải:

Kí hiệu A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Sử dụng biểu đồ Ven, minh họa tập hợp các khán giả đã tham gia bình chọn (𝐴∪𝐵) và các khán giả không tham gia bình chọn.

Gọi A, B lần lượt là tập hợp các khán giả bình chọn cho thí sinh A và thí sinh B.

Theo giả thiết, 𝑛(𝐴)=85,𝑛(𝐵)=72,𝑛(𝐴∩𝐵)=60

Nhận thấy rằng, nếu tính tổng 𝑛(𝐴)+𝑛(𝐵) thì ta được số khán giả đã tham gia bình chọn, nhưng số khán giả bình chọn cho cả hai thí sinh được tính hai lần. Do đó, số khán giả đã tham gia bình chọn là:

𝑛(𝐴∪𝐵)=𝑛(𝐴)+𝑛(𝐵)−𝑛(𝐴∩𝐵)=85+72−60=97
Như vậy trong hội trường 100 khán giả, có 97 khán giải đã tham gia bình chọn, còn lại số khán giả không tham gia bình chọn là: 100−97=3 (khán giả).

Trở lại bảng thông tin về kết quả phỏng vấn tuyển dụng ở Hoạt động khám phá 1.

a) Xác định tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ.

b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn.

Phương pháp giải:

Viết tập hợp bằng cách liệt kê các phần tử.

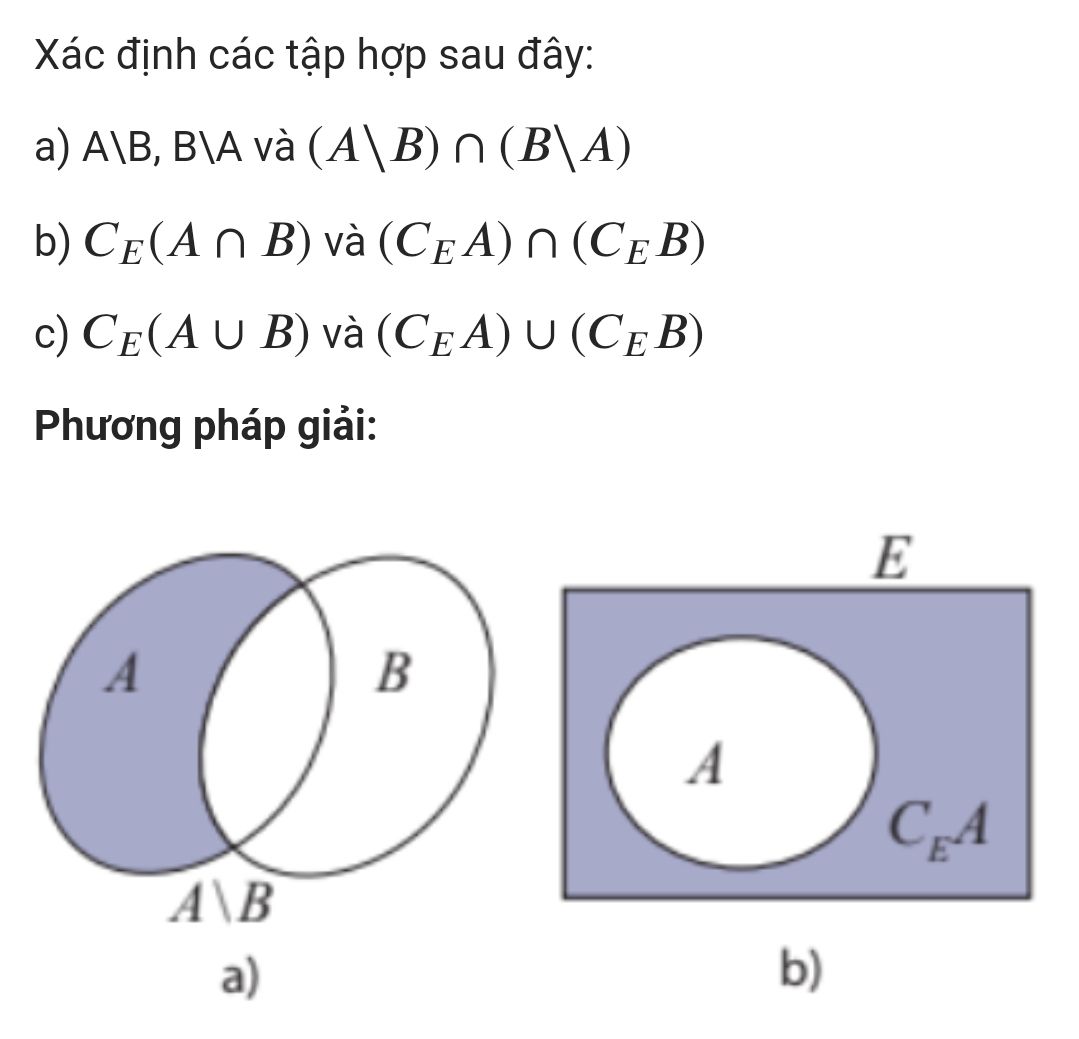
Cho tập hợp 𝐸={𝑥∈ℕ|𝑥<8},𝐴={0;1;2;3;4},𝐵={3;4;5}